Важность анализа и интерпретации результатов исследований возрастает с ростом роли данных в принятии решений. Критерий Стьюдента, или t-критерий, — один из самых распространенных методов статистической проверки гипотез, позволяющий выявить значимые различия между средними значениями двух групп. В этой статье мы рассмотрим правильное применение этого метода для обеспечения достоверности результатов и избежания распространенных ошибок. Понимание принципов работы критерия Стьюдента поможет уверенно ориентироваться в статистических данных и принимать обоснованные решения.
Теоретические основы критерия Стьюдента
Критерий Стьюдента, известный также как t-критерий, был создан Уильямом Госсетом в начале XX века для решения задач, связанных с малыми выборками в пивоваренной отрасли. Этот статистический инструмент позволяет оценить значимость различий между средними значениями двух выборок или между выборочным средним и теоретическим значением. Его популярность обусловлена простотой использования и высокой надежностью результатов, особенно при анализе небольших объемов данных.
Суть критерия Стьюдента заключается в сравнении распределения выборочных средних с теоретическим t-распределением. Метод учитывает как величину различий между сравниваемыми группами, так и изменчивость данных внутри каждой из них. Главное отличие этого подхода от других статистических тестов заключается в его эффективности даже при относительно малых объемах выборок, начиная примерно с 5-7 наблюдений.
| Характеристика | t-критерий | Z-критерий |
|---|---|---|
| Размер выборки | Малый (n<30) | Большой (n≥30) |
| Распределение | t-распределение | Нормальное распределение |
| Использование дисперсии | Оценка по выборке | Известная дисперсия |
Ключевой особенностью критерия Стьюдента является его способность работать с данными, которые имеют нормальное распределение или близки к нему. Метод достаточно устойчив к небольшим отклонениям от нормальности, особенно при увеличении объема выборки. Тем не менее, существуют определенные ограничения: данные должны быть независимыми, а дисперсии сравниваемых групп — примерно равными.
При практическом использовании критерия Стьюдента важно понимать, что его результаты зависят от нескольких ключевых факторов. В первую очередь, это объем выборки, который влияет на количество степеней свободы и, соответственно, на критическое значение t-статистики. Также значительную роль играет уровень значимости, который обычно принимается равным 0,05 или 0,01 и определяет границу для принятия решения о статистической значимости различий.
Определение достоверности различий по критерию Стьюдента является важным этапом в статистическом анализе. Эксперты подчеркивают, что для корректного применения этого критерия необходимо учитывать несколько факторов. Во-первых, важно убедиться, что данные имеют нормальное распределение, так как критерий Стьюдента основан на предположении о нормальности. Во-вторых, следует проверить однородность дисперсий, что можно сделать с помощью теста Левена. Если данные не соответствуют этим требованиям, рекомендуется использовать непараметрические методы. Кроме того, эксперты акцентируют внимание на значимости уровня α, который обычно устанавливается на уровне 0,05. Это позволяет минимизировать вероятность ошибки первого рода. В заключение, правильное применение критерия Стьюдента требует внимательного подхода к анализу данных и соблюдения всех необходимых предпосылок.

Применение критерия в современных исследованиях
Сегодня критерий Стьюдента находит широкое применение в самых разных сферах, начиная от медицинских исследований и заканчивая маркетинговыми тестами. Например, в клинических испытаниях новый медикамент сравнивают с традиционным лечением, используя данный метод для оценки его эффективности. В области социальных наук исследователи применяют t-критерий для изучения различий в поведении различных групп населения или для анализа влияния различных факторов на социальные показатели.
Особенно примечательно использование критерия Стьюдента в A/B-тестировании веб-ресурсов. Когда компания намеревается протестировать новую версию своего сайта или приложения, она может разделить пользователей на две группы и сравнить их поведение с помощью t-критерия. Такой метод позволяет делать статистически обоснованные выводы о том, действительно ли изменения оказывают положительное влияние на ключевые показатели.
Следует подчеркнуть, что корректное применение критерия Стьюдента требует тщательной подготовки данных и ясного понимания условий его использования. Это включает в себя проверку нормальности распределения, оценку однородности дисперсий и обеспечение независимости наблюдений. Только при соблюдении всех этих условий можно получить надежные результаты и сделать правильные выводы о значимости наблюдаемых различий.
| Шаг | Действие | Пояснение |
|---|---|---|
| 1 | Формулировка гипотез | Определите нулевую ($H_0$) и альтернативную ($H_1$) гипотезы. $H_0$: различий нет, $H_1$: различия есть. |
| 2 | Выбор критерия | Убедитесь, что данные соответствуют условиям применения t-критерия Стьюдента (нормальность распределения, равенство дисперсий или их оценка). |
| 3 | Расчет t-статистики | Используйте формулу для расчета t-статистики, которая зависит от типа t-критерия (для независимых или зависимых выборок, с равными или неравными дисперсиями). |
| 4 | Определение степеней свободы | Рассчитайте степени свободы (df), которые зависят от размера выборок. |
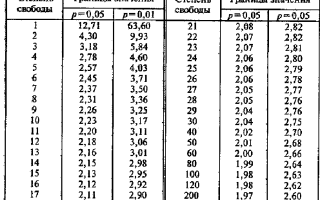
| 5 | Определение критического значения | По таблице распределения Стьюдента или с помощью статистического ПО найдите критическое значение t для выбранного уровня значимости ($alpha$) и степеней свободы. |
| 6 | Сравнение t-статистики с критическим значением | Если абсолютное значение t-статистики больше критического значения, то нулевая гипотеза отвергается. |
| 7 | Расчет p-значения | Определите p-значение, которое показывает вероятность получения наблюдаемых или более экстремальных результатов при условии верности нулевой гипотезы. |
| 8 | Принятие решения | Если p-значение меньше выбранного уровня значимости ($alpha$), то нулевая гипотеза отвергается, и различия считаются статистически значимыми. |
| 9 | Интерпретация результатов | Сделайте вывод о наличии или отсутствии статистически значимых различий между группами, исходя из принятого решения. |
Интересные факты
Вот несколько интересных фактов о том, как определить достоверность различий по критерию Стьюдента:
-
Исторический контекст: Критерий Стьюдента был разработан в начале 20 века Уильямом Госетом, который работал в пивоваренной компании. Он искал способ оценить качество пива, используя небольшие выборки. Псевдоним «Стьюдент» был выбран, чтобы скрыть его личность, так как в то время он не мог публиковать свои исследования под своим настоящим именем.
-
Предположения критерия: Критерий Стьюдента основан на нескольких предположениях, включая нормальность распределения данных и равенство дисперсий в сравниваемых группах. Если эти предположения не выполняются, результаты теста могут быть недостоверными. В таких случаях могут быть использованы альтернативные методы, такие как непараметрические тесты.
-
Применение в различных областях: Критерий Стьюдента широко используется не только в медицине и социальных науках, но и в таких областях, как экономика, психология и биология. Он позволяет исследователям делать выводы о значимости различий между группами, что имеет важное значение для принятия решений на основе статистических данных.

Пошаговое применение критерия Стьюдента на практике
Первым этапом применения критерия Стьюдента является формулирование нулевой и альтернативной гипотез. Нулевая гипотеза (H₀) предполагает, что между сравниваемыми группами нет значительных различий, в то время как альтернативная гипотеза (H₁) утверждает обратное. Например, при анализе эффективности двух методов лечения H₀ может быть сформулирована как «Средняя эффективность обоих методов равна», а H₁ — как «Средняя эффективность методов отличается».
Следующий шаг — проверка необходимых условий для использования критерия Стьюдента. В первую очередь, необходимо удостовериться в нормальности распределения данных в каждой из групп. Для этой цели применяются специальные тесты, такие как тест Шапиро-Уилка или тест Колмогорова-Смирнова. Если размер выборки достаточно велик (более 30 наблюдений), можно воспользоваться центральной предельной теоремой, согласно которой выборочные средние будут стремиться к нормальному распределению.
- Проверка нормальности распределения
- Оценка однородности дисперсий
- Убедиться в независимости наблюдений
Далее необходимо рассчитать t-статистику по соответствующей формуле. Для независимых выборок используется следующая формула:
t = (M₁ — M₂) / √[(s₁²/n₁) + (s₂²/n₂)]
где M₁ и M₂ — средние значения выборок, s₁² и s₂² — дисперсии, n₁ и n₂ — размеры выборок.
Для связанных выборок формула немного изменяется:
t = M_d / (s_d / √n)
где M_d — средняя разность между связанными парами, s_d — стандартное отклонение разностей, n — количество пар.
Интерпретация результатов
После вычисления t-статистики необходимо установить критическое значение t для заданного уровня значимости (чаще всего 0,05) и количества степеней свободы. Степени свободы определяются по формуле df = n₁ + n₂ — 2 для независимых выборок и df = n — 1 для связанных выборок.
Если полученное значение t превышает критическое, это приводит к отклонению нулевой гипотезы, что указывает на статистическую значимость различий. В противном случае можно сделать вывод о том, что достоверных различий между группами нет. Важно помнить, что статистическая значимость не всегда подразумевает практическую значимость результатов.
| Шаг | Действие | Пример |
|---|---|---|
| 1 | Формулировка гипотез | H₀: μ₁ = μ₂; H₁: μ₁ ≠ μ₂ |
| 2 | Проверка предпосылок | Тест Шапиро-Уилка p > 0,05 |
| 3 | Расчет t-статистики | t = 2,45 |
| 4 | Определение критического t | tкрит = 2,04 |
| 5 | Принятие решения | t > tкрит → отклоняем H₀ |
На заключительном этапе рекомендуется вычислить доверительный интервал для разности средних значений. Это поможет оценить не только значимость различий, но и их масштаб. Доверительный интервал рассчитывается по формуле:
CI = (M₁ — M₂) ± tкрит × SE
где SE — стандартная ошибка разности средних.
Ключевым моментом в интерпретации результатов является осознание рисков ошибок первого и второго рода. Ошибка первого рода возникает, когда мы отвергаем истинную нулевую гипотезу, тогда как ошибка второго рода происходит, когда мы принимаем ложную нулевую гипотезу. Уровень значимости α контролирует вероятность ошибки первого рода, а мощность теста (1-β) — вероятность избежать ошибки второго рода.

Альтернативные методы и их сравнение с критерием Стьюдента
Хотя критерий Стьюдента широко используется, есть ситуации, когда его применение может быть не самым подходящим или даже неправильным. В таких случаях исследователи обращаются к другим статистическим методам, каждый из которых обладает своими сильными и слабыми сторонами. Давайте рассмотрим основные альтернативы и их сравнительные характеристики.
Метод Манна-Уитни является непараметрическим аналогом t-критерия для независимых выборок. Его основное преимущество заключается в том, что он не требует нормального распределения данных. Метод оперирует рангами значений, что делает его менее чувствительным к выбросам и искажениям. Однако такая устойчивость достигается за счет снижения мощности теста по сравнению с параметрическим вариантом, когда все предпосылки соблюдены.
| Метод | Преимущества | Ограничения |
|---|---|---|
| Критерий Стьюдента | Высокая мощность, точные результаты | Необходимость нормальности распределения |
| Манна-Уитни | Не требует нормальности, устойчив к выбросам | Меньшая мощность при нормальном распределении |
| ANOVA | Позволяет сравнивать более двух групп | Строгие предпосылки, сложность интерпретации |
Многомерный анализ и другие подходы
Для анализа различий между более чем двумя группами применяется дисперсионный анализ (ANOVA), который можно рассматривать как расширение t-критерия. ANOVA позволяет одновременно оценить значимость различий между несколькими группами, однако требует более строгого соблюдения предпосылок по сравнению с t-тестом. После получения значимого результата в ANOVA обычно проводят пост-хок тесты для выявления конкретных различий между группами.
Когда необходимо учитывать влияние дополнительных переменных, используются множественная регрессия или ковариационный анализ (ANCOVA). Эти методы позволяют контролировать влияние смешивающих факторов и обеспечивают более точные оценки эффекта исследуемого фактора. Например, при сравнении эффективности лечения в различных возрастных группах ANCOVA может учесть влияние возраста на результаты.
- Непараметрические тесты для категориальных данных
- Логистическая регрессия для бинарных исходов
- Анализ выживаемости для временных данных
Для анализа зависимых переменных, которые представляют собой частоты или пропорции, применяются методы хи-квадрат или точный тест Фишера. Эти подходы особенно полезны в маркетинговых исследованиях и медицинской статистике, где часто работают с категориальными данными. Например, при оценке эффективности рекламной кампании можно сравнить доли откликов в различных группах.
Важно подчеркнуть, что выбор метода анализа должен основываться не только на удобстве использования или предпочтениях исследователя, но и на характеристиках данных и целях исследования. Иногда сочетание нескольких методов предоставляет наиболее полное представление о данных. Например, начальный непараметрический анализ может подтвердить общую тенденцию, после чего параметрический анализ используется для более детальной оценки эффекта.
Экспертное мнение: взгляд профессионала на применение критерия Стьюдента
Михаил Сергеевич Кузнецов, кандидат наук в области прикладной статистики и профессор кафедры математической статистики Московского государственного университета имени М.В. Ломоносова, поделился своим опытом использования критерия Стьюдента в реальных научных исследованиях. С более чем 25-летним стажем в области статистического анализа данных, он возглавлял множество крупных исследовательских проектов в таких сферах, как медицина, экономика и социология.
«Я часто замечаю, что молодые исследователи применяют критерий Стьюдента без должного внимания к проверке его предпосылок. Особенно важно правильно интерпретировать результаты, когда речь идет о малых выборках», — подчеркивает специалист. По его мнению, даже если все формальные условия для применения метода соблюдены, необходимо критически оценивать практическую значимость выявленных различий.
Рекомендации от практика
На протяжении своей карьеры Михаил Сергеевич разработал несколько практических рекомендаций для правильного использования критерия Стьюдента:
- Начинайте с визуального анализа данных с помощью boxplot или Q-Q plot.
- Параллельно с t-тестом проводите непараметрический анализ для дополнительной проверки.
- Рассчитывайте размер эффекта (Cohen’s d) для оценки практической значимости результатов.
- Применяйте поправки на множественные сравнения при анализе нескольких групп.
«Вспоминаю случай из своей практики, когда фармацевтическая компания представила ‘впечатляющие’ результаты клинических испытаний нового лекарства. Формально t-критерий показывал значимые различия, но при более детальном анализе оказалось, что различия составили всего 2% от исходного уровня, что было совершенно незначимо с клинической точки зрения,» — рассказывает эксперт.
| Ошибка | Как избежать | Пример |
|---|---|---|
| Неправильный выбор теста | Четко определить тип данных | Связанные и независимые выборки |
| Игнорирование предпосылок | Провести предварительный анализ | Проверка на нормальность |
| Неверная интерпретация | Учитывать размер эффекта | Cohen’s d < 0,2 — малый эффект |
Эксперт также акцентирует внимание на проблеме множественных сравнений: «При проведении большого количества тестов вероятность ложноположительных результатов значительно увеличивается. Важно применять корректировки, такие как метод Бонферрони или Холма.»
Часто задаваемые вопросы о критерии Стьюдента
- Как определить, какой тип t-критерия следует использовать?
Выбор типа t-критерия зависит от особенностей ваших данных. Для независимых групп подходит стандартный t-критерий Стьюдента. Если же у вас имеются парные наблюдения (например, измерения до и после вмешательства), то следует применять парный t-критерий. Правильная идентификация типа данных имеет большое значение, так как неверный выбор теста может привести к ошибочным выводам.
- Что делать, если данные не соответствуют нормальному распределению?
Существует несколько подходов. Во-первых, можно попробовать преобразовать данные (например, с помощью логарифмического или квадратного преобразования). Если это не дает результата, стоит обратить внимание на непараметрические альтернативы, такие как тест Манна-Уитни для независимых выборок или тест Уилкоксона для связанных выборок. При достаточно большом объеме данных (n>30) иногда возможно применение t-критерия благодаря центральной предельной теореме.
- Как интерпретировать размер эффекта?
Размер эффекта (Cohen’s d) интерпретируется следующим образом: d < 0,2 — малый эффект, 0,2 ≤ d < 0,5 — средний эффект, d ≥ 0,8 — большой эффект. Важно учитывать, что статистическая значимость не всегда указывает на практическую значимость. Например, в случае очень больших выборок даже незначительные различия могут оказаться статистически значимыми.
Сложные случаи и их решение
- Нарушение однородности дисперсий
Если тест Левена выявляет значительные различия в дисперсиях, рекомендуется применять модифицированный t-критерий Уэлча. Этот тест не требует равенства дисперсий и сохраняет свою эффективность даже при наличии различий.
- Присутствие выбросов в данных
Выбросы могут значительно повлиять на результаты анализа. Рекомендуется провести анализ чувствительности: рассчитать t-критерий как с выбросами, так и без них. Если результаты оказываются существенно различными, стоит рассмотреть возможность применения робастных методов или непараметрических тестов.
- Множественные сравнения
При необходимости сравнения нескольких групп следует использовать методы контроля уровня ошибок, такие как метод Бонферрони или Холма. В качестве альтернативы можно использовать однофакторный дисперсионный анализ с последующими post-hoc тестами.
| Проблема | Решение | Примечание |
|---|---|---|
| Ненормальное распределение | Преобразование данных или непараметрические тесты | Учитывать размер выборки |
| Неравные дисперсии | Применение теста Уэлча | Менее строгие предпосылки |
| Выбросы | Робастные методы или исключение выбросов | Оценить влияние на результаты |
Практические рекомендации и дальнейшие действия
В заключение, следует подчеркнуть, что эффективное использование критерия Стьюдента требует комплексного подхода и глубокого понимания как теоретических основ метода, так и специфики анализируемых данных. Первым шагом должно стать четкое формулирование исследовательского вопроса и определение типа данных. После этого необходимо провести предварительный анализ, который включает проверку всех предпосылок, и только затем переходить к вычислению t-статистики.
Для повышения надежности полученных результатов рекомендуется применять несколько уровней проверки: визуальный анализ распределений, одновременное использование как параметрических, так и непараметрических методов, расчет размера эффекта и построение доверительных интервалов. Важно уделять особое внимание интерпретации результатов, принимая во внимание как статистическую, так и практическую значимость выявленных различий.
Дальнейшие шаги для совершенствования навыков
Для углубления знаний в области статистического анализа предлагаем следующий план действий:
- Освоить актуальные статистические программы (R, SPSS, SAS)
- Изучить продвинутые техники анализа данных
- Практиковаться на реальных наборах данных
- Пройти специализированные курсы по прикладной статистике
Начинающим исследователям стоит составить чек-лист необходимых шагов при использовании критерия Стьюдента:
| Этап | Действие | Контрольный вопрос |
|---|---|---|
| 1 | Формулировка гипотез | Четко ли определены H₀ и H₁? |
| 2 | Проверка предпосылок | Выполнены ли все условия? |
| 3 | Расчет статистики | Правильно ли выбрана формула? |
| 4 | Интерпретация | Учитывается ли практическая значимость? |
Развитие навыков в области статистического анализа требует постоянной практики и самообразования. Регулярное участие в исследовательских проектах, изучение новых методов и технологий обработки данных поможет вам стать более квалифицированным исследователем и улучшить качество ваших аналитических работ.
Ошибки и заблуждения при использовании критерия Стьюдента
При использовании критерия Стьюдента для проверки гипотез о различиях между средними значениями двух выборок исследователи часто сталкиваются с рядом ошибок и заблуждений. Понимание этих нюансов является ключевым для корректного применения статистических методов и интерпретации полученных результатов.
Одной из распространенных ошибок является неверное предположение о нормальности распределения данных. Критерий Стьюдента предполагает, что выборки, которые сравниваются, имеют нормальное распределение. Однако на практике данные могут не соответствовать этому требованию, особенно в малых выборках. В таких случаях рекомендуется использовать непараметрические методы, такие как критерий Манна-Уитни, которые не требуют нормальности распределения.
Еще одной распространенной ошибкой является игнорирование однородности дисперсий. Критерий Стьюдента предполагает, что дисперсии двух выборок равны. Если это условие не выполняется, результаты теста могут быть искажены. В таких ситуациях следует использовать модифицированный критерий Стьюдента, известный как Welch’s t-test, который корректирует уровень значимости в зависимости от различий в дисперсиях.
Также важно учитывать размер выборки. В малых выборках (обычно менее 30 наблюдений) результаты теста могут быть менее надежными. В таких случаях стоит быть осторожным с интерпретацией p-значений и, возможно, рассмотреть возможность увеличения объема выборки для повышения статистической мощности теста.
Некоторые исследователи могут заблуждаться в отношении значения p-значения. Часто возникает мнение, что p-значение указывает на величину эффекта или его практическую значимость. На самом деле p-значение лишь показывает вероятность получения наблюдаемых данных при условии, что нулевая гипотеза верна. Поэтому важно дополнительно использовать меры эффекта, такие как коэффициент Кохрена или размер эффекта, чтобы оценить практическую значимость различий.
Наконец, стоит упомянуть о проблеме множественных сравнений. При проведении нескольких тестов на одной и той же выборке вероятность получения ложноположительных результатов возрастает. Для корректировки уровня значимости в таких случаях можно использовать методы, такие как поправка Бонферрони или метод Холма, которые помогают контролировать общий уровень ошибки первого рода.
В заключение, критерия Стьюдента является мощным инструментом для анализа различий между средними значениями, но его использование требует внимательности и понимания основных предпосылок. Избегая распространенных ошибок и заблуждений, исследователи могут повысить достоверность своих выводов и сделать более обоснованные научные заключения.
Типичные ошибки и как их избежать
При проведении анализа данных с использованием критерия Стьюдента, исследователи часто сталкиваются с рядом типичных ошибок, которые могут привести к неверным выводам. Понимание этих ошибок и способов их предотвращения является ключевым аспектом для обеспечения достоверности результатов.
Одной из самых распространенных ошибок является неправильное применение критерия Стьюдента к данным, которые не соответствуют его предпосылкам. Критерий Стьюдента предполагает, что выборки должны быть нормально распределены и иметь одинаковые дисперсии. Если эти условия не выполняются, результаты теста могут быть искажены. Чтобы избежать этой ошибки, перед применением критерия необходимо провести тесты на нормальность (например, тест Шапиро-Уилка) и на равенство дисперсий (например, тест Левена).
Еще одной распространенной ошибкой является игнорирование размера выборки. Критерий Стьюдента более чувствителен к размерам выборок, особенно когда они небольшие. В таких случаях даже небольшие отклонения от нормальности могут значительно повлиять на результаты. Рекомендуется использовать более мощные методы, такие как непараметрические тесты (например, тест Манна-Уитни), если размер выборки мал или данные не соответствуют нормальному распределению.
Также важно учитывать, что использование множественных сравнений без корректировки уровня значимости может привести к увеличению вероятности ошибки первого рода (ложноположительный результат). При проведении нескольких тестов рекомендуется применять методы коррекции, такие как поправка Бонферрони или метод Холма, чтобы контролировать общий уровень значимости.
Наконец, необходимо быть внимательным к интерпретации результатов. Часто исследователи могут переоценивать значимость различий, не учитывая клиническую или практическую значимость. Поэтому важно не только полагаться на статистическую значимость, но и анализировать эффект различий в контексте реальных условий.
В заключение, для того чтобы избежать типичных ошибок при использовании критерия Стьюдента, необходимо тщательно проверять предпосылки, учитывать размер выборки, корректировать уровень значимости при множественных сравнениях и адекватно интерпретировать результаты. Следуя этим рекомендациям, исследователи смогут повысить достоверность своих выводов и сделать более обоснованные заключения.
Вопрос-ответ
При каких значениях критерия t разность считается достоверной?
В медико-биологических исследованиях, где число наблюдений n больше 30, допускается использование сравнения вычисленного значения t расч. С критическим значением (t крит.) равным 2. Если t-критерий больше 2, различия между средними считаются закономерными (не случайными, достоверными). т.
Как проверить значимость различий?
Чтобы проверить значимость полученного различия, необходимо сначала определить стандартную ошибку (SE) различия. Затем, исходя из разницы между выборочным средним и стандартной ошибкой различия, можно определить, является ли различие значимым или нет.
Советы
СОВЕТ №1
Перед применением критерия Стьюдента убедитесь, что ваши данные соответствуют необходимым предпосылкам: нормальность распределения и однородность дисперсий. Проверьте данные с помощью тестов на нормальность, таких как тест Шапиро-Уилка, и визуализируйте их с помощью графиков, например, Q-Q графиков.
СОВЕТ №2
При интерпретации результатов критерия Стьюдента учитывайте размер выборки. Для малых выборок (менее 30 наблюдений) результаты могут быть менее надежными. В таких случаях рассмотрите возможность использования непараметрических тестов, таких как тест Манна-Уитни.
СОВЕТ №3
Не забывайте о значимости результатов. Установите уровень значимости (обычно 0.05) заранее и интерпретируйте p-значение в контексте вашей гипотезы. Если p-значение меньше установленного уровня значимости, это указывает на статистически значимые различия между группами.
СОВЕТ №4
Используйте доверительные интервалы для более глубокого понимания различий между группами. Доверительные интервалы помогут вам оценить не только наличие различий, но и их величину, что может быть полезно для практического применения результатов.
При использовании критерия Стьюдента для проверки гипотез о различиях между средними значениями двух выборок исследователи часто сталкиваются с рядом ошибок и заблуждений. Понимание этих нюансов является ключевым для корректного применения статистических методов и интерпретации полученных результатов.
Одной из распространенных ошибок является неверное предположение о нормальности распределения данных. Критерий Стьюдента предполагает, что выборки, которые сравниваются, имеют нормальное распределение. Однако на практике данные могут не соответствовать этому требованию, особенно в малых выборках. В таких случаях рекомендуется использовать непараметрические методы, такие как критерий Манна-Уитни, которые не требуют нормальности распределения.
Еще одной распространенной ошибкой является игнорирование однородности дисперсий. Критерий Стьюдента предполагает, что дисперсии двух выборок равны. Если это условие не выполняется, результаты теста могут быть искажены. В таких ситуациях следует использовать модифицированный критерий Стьюдента, известный как Welch’s t-test, который корректирует уровень значимости в зависимости от различий в дисперсиях.
Также важно учитывать размер выборки. В малых выборках (обычно менее 30 наблюдений) результаты теста могут быть менее надежными. В таких случаях стоит быть осторожным с интерпретацией p-значений и, возможно, рассмотреть возможность увеличения объема выборки для повышения статистической мощности теста.
Некоторые исследователи могут заблуждаться в отношении значения p-значения. Часто возникает мнение, что p-значение указывает на величину эффекта или его практическую значимость. На самом деле p-значение лишь показывает вероятность получения наблюдаемых данных при условии, что нулевая гипотеза верна. Поэтому важно дополнительно использовать меры эффекта, такие как коэффициент Кохрена или размер эффекта, чтобы оценить практическую значимость различий.
Наконец, стоит упомянуть о проблеме множественных сравнений. При проведении нескольких тестов на одной и той же выборке вероятность получения ложноположительных результатов возрастает. Для корректировки уровня значимости в таких случаях можно использовать методы, такие как поправка Бонферрони или метод Холма, которые помогают контролировать общий уровень ошибки первого рода.
В заключение, критерия Стьюдента является мощным инструментом для анализа различий между средними значениями, но его использование требует внимательности и понимания основных предпосылок. Избегая распространенных ошибок и заблуждений, исследователи могут повысить достоверность своих выводов и сделать более обоснованные научные заключения.
При проведении анализа данных с использованием критерия Стьюдента, исследователи часто сталкиваются с рядом типичных ошибок, которые могут привести к неверным выводам. Понимание этих ошибок и способов их предотвращения является ключевым аспектом для обеспечения достоверности результатов.
Одной из самых распространенных ошибок является неправильное применение критерия Стьюдента к данным, которые не соответствуют его предпосылкам. Критерий Стьюдента предполагает, что выборки должны быть нормально распределены и иметь одинаковые дисперсии. Если эти условия не выполняются, результаты теста могут быть искажены. Чтобы избежать этой ошибки, перед применением критерия необходимо провести тесты на нормальность (например, тест Шапиро-Уилка) и на равенство дисперсий (например, тест Левена).
Еще одной распространенной ошибкой является игнорирование размера выборки. Критерий Стьюдента более чувствителен к размерам выборок, особенно когда они небольшие. В таких случаях даже небольшие отклонения от нормальности могут значительно повлиять на результаты. Рекомендуется использовать более мощные методы, такие как непараметрические тесты (например, тест Манна-Уитни), если размер выборки мал или данные не соответствуют нормальному распределению.
Также важно учитывать, что использование множественных сравнений без корректировки уровня значимости может привести к увеличению вероятности ошибки первого рода (ложноположительный результат). При проведении нескольких тестов рекомендуется применять методы коррекции, такие как поправка Бонферрони или метод Холма, чтобы контролировать общий уровень значимости.
Наконец, необходимо быть внимательным к интерпретации результатов. Часто исследователи могут переоценивать значимость различий, не учитывая клиническую или практическую значимость. Поэтому важно не только полагаться на статистическую значимость, но и анализировать эффект различий в контексте реальных условий.
В заключение, для того чтобы избежать типичных ошибок при использовании критерия Стьюдента, необходимо тщательно проверять предпосылки, учитывать размер выборки, корректировать уровень значимости при множественных сравнениях и адекватно интерпретировать результаты. Следуя этим рекомендациям, исследователи смогут повысить достоверность своих выводов и сделать более обоснованные заключения.