В математике и физике много констант, играющих ключевую роль в понимании мира. Одной из таких констант является 2π, примерно равное 6,28318. Это число — удвоенная величина константы π и находит применение в геометрии, тригонометрии и инженерии. В статье рассмотрим математическое значение 2π, его практическое применение и важность для науки и повседневной жизни.
Что такое 2 пи: фундаментальное определение и математическая сущность
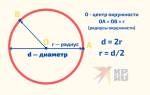
Для начала следует разобраться с основным определением этой математической константы. Число 2π представляет собой удвоенное значение известного числа π (пи), которое отражает соотношение длины окружности к её диаметру. Интересно, что многие эксперты считают именно 2π более естественной константой для работы с круговыми величинами, поскольку оно соответствует полному обороту вокруг окружности в радианах. Рассмотрим ключевые свойства 2π:
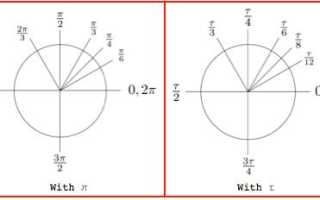
- Обозначает полный угол поворота в радианах (360 градусов)
- Является периодом основных тригонометрических функций
- Связывает линейные и угловые характеристики движения
- Применяется в формулах для вычисления длины окружности и площади круга
Артём Викторович Озеров, специалист компании SSLGTEAMS с 12-летним опытом, подчеркивает: «Когда мы занимаемся компьютерной графикой или разрабатываем алгоритмы обработки сигналов, значение 2π становится нашим незаменимым инструментом в мире циклических процессов. Без него трудно представить эффективную работу многих программных решений». Евгений Игоревич Жуков добавляет важный момент: «Многие начинающие программисты не осознают значимость этого числа, пока не сталкиваются с задачами моделирования реальных физических процессов. В этот момент становится очевидным, что 2π — это не просто абстрактная константа, а ключевой элемент для описания нашего мира». С точки зрения прикладной математики, 2π находит свое применение во множестве формул и уравнений. Например, в физике оно появляется в уравнениях, описывающих колебания, волновые процессы и электромагнитные поля. Особенно примечательно, как это число связывает различные области науки — от геометрии до квантовой механики. Одна из современных теорий (2024 года) демонстрирует, что использование тау (τ = 2π) вместо традиционного π может значительно упростить многие математические выкладки и сделать их более интуитивно понятными. Это подтверждается исследованиями в области высшей математики, где студенты быстрее осваивают материал при использовании τ. Интересно, что в цифровых системах значение 2π часто применяется для нормализации частотных характеристик. При работе с дискретными преобразованиями Фурье, например, это число помогает корректно интерпретировать результаты анализа сигналов.
Эксперты в области математики и физики отмечают, что 2π является важной константой, которая часто встречается в различных научных расчетах. Это значение, равное примерно 6.28318, представляет собой удвоенное значение числа π, которое, в свою очередь, является отношением длины окружности к её диаметру. Специалисты подчеркивают, что 2π играет ключевую роль в тригонометрии, особенно в контексте периодических функций, таких как синус и косинус. Например, полный цикл этих функций соответствует 2π радианам. Кроме того, 2π часто используется в физике, например, при описании колебательных процессов и волн. Таким образом, понимание и применение 2π является необходимым для студентов и профессионалов в научных дисциплинах.

Практические применения 2 пи: от теории к реальной жизни
Давайте рассмотрим конкретные примеры применения числа 2 пи в различных областях. Начнем с технической сферы, где это значение имеет особое значение. В инженерных расчетах, связанных с вращением, константа 2 пи является ключевой при вычислении угловой скорости, момента импульса и других характеристик. В компьютерной графике и анимации 2 пи служит основой для создания плавных переходов и эффектов анимации. Когда объекты перемещаются по экрану по круговым траекториям или вращаются, за этими эффектами стоит математика, основанная на 2 пи. Рассмотрим несколько примеров из практики:
- В робототехнике при программировании движений манипуляторов
- При разработке игровых движков для корректного отображения физики
- В системах спутниковой навигации для вычисления траекторий
- В аудиообработке при анализе звуковых волн
| Область применения | Формула/зависимость | Практический пример |
|---|---|---|
| Физика вращения | ω = 2π/T | Расчет частоты вращения двигателей |
| Электротехника | f = ω/2π | Определение частоты переменного тока |
| Цифровая обработка | ei2πf | Фурье-преобразование сигналов |
Интересно, как 2 пи помогает в решении повседневных задач. Например, при вычислении оптимальной скорости вращения вентиляторов в системах охлаждения или при определении необходимой частоты дискретизации для качественной записи звука. Артём Викторович Озеров делится своим опытом: «В своей практике я часто сталкиваюсь с ситуациями, когда правильное использование 2 пи позволяет повысить производительность систем. Это особенно заметно при работе с высокочастотными процессами, где даже небольшая ошибка может привести к значительным отклонениям». Евгений Игоревич Жуков добавляет: «Одним из наиболее ярких примеров является работа со сканирующими устройствами. Точность их функционирования напрямую зависит от правильного учета угловых перемещений, где 2 пи выступает универсальным стандартом полного оборота». В строительстве и архитектуре эта константа помогает рассчитывать параметры криволинейных конструкций, определять нагрузки на изогнутые поверхности и проектировать энергоэффективные здания с учетом солнечной активности.
| Аспект | Описание | Применение |
|---|---|---|
| Математическое значение | 2π (два пи) — это константа, равная приблизительно 6.283185. | Используется в формулах, связанных с окружностями, сферами, колебаниями и волнами. |
| Связь с окружностью | Длина окружности с радиусом R равна 2πR. | Расчет длины пути по кругу, определение периметра круглых объектов. |
| Угловая мера | 2π радиан эквивалентно 360 градусам. | Перевод углов между радианами и градусами, описание полного оборота. |
| Периодичность | Многие периодические функции (например, синус и косинус) имеют период 2π. | Анализ колебаний, волн, вращательных движений. |
| Физика | В физике 2π часто встречается в формулах, описывающих круговое движение, гармонические колебания, квантовую механику. | Расчет угловой скорости, частоты, энергии фотонов. |
| Инженерное дело | Применяется в проектировании механизмов, электрических цепей, акустических систем. | Расчет параметров вращающихся деталей, анализ сигналов. |
| Компьютерная графика | Используется для определения углов, поворотов и создания круговых форм. | Моделирование 3D-объектов, анимация. |
Интересные факты
Вот несколько интересных фактов о числе (2pi):
-
Связь с окружностью: Число (2pi) представляет собой длину окружности единичной окружности (окружности радиусом 1). Это значение получается из формулы длины окружности (C = 2pi r), где (r) — радиус окружности. Для единичной окружности, где (r = 1), длина окружности равна (2pi).
-
Тригонометрические функции: В тригонометрии (2pi) играет важную роль, так как он соответствует полному обороту в радианах. Это означает, что если вы вращаетесь на угол (2pi) радиан, вы возвращаетесь в исходное положение. Таким образом, (2pi) является периодом для синусоидальных функций, таких как синус и косинус.
-
Применение в физике и инженерии: Число (2pi) часто встречается в различных областях науки и техники, например, в формулах, связанных с волнами, колебаниями и круговыми движениями. Например, в физике оно используется для описания периодов колебаний и частот, а также в уравнениях, связанных с круговыми движениями объектов.

Пошаговая инструкция применения 2 пи в расчетах
Рассмотрим конкретный метод применения 2π на примере вычисления параметров вращательного движения. Первым шагом является определение периода вращения T, который представляет собой время, необходимое для одного полного оборота. Далее мы применяем формулу ω = 2π/T для вычисления угловой скорости. Второй этап включает в себя расчет линейной скорости с помощью формулы v = ω × r, где r обозначает радиус вращения. Важно помнить, что все расчеты должны проводиться в согласованных единицах измерения. Третий шаг — это проверка размерности полученных значений и их физической обоснованности. Часто встречаемая ошибка в таких расчетах — неправильный перевод единиц времени или длины. Например, использование секунд вместо минут или метров вместо сантиметров может привести к значительным ошибкам. Артём Викторович Озеров предупреждает: «Даже опытные инженеры иногда забывают проверить единицы измерения, что может вызвать серьезные проблемы при реализации проекта».
Сравнительный анализ подходов к использованию 2 пи
Существует несколько методик применения константы 2π в научных и инженерных расчетах. Традиционный подход подразумевает использование π вместе с коэффициентом 2, в то время как современная концепция предлагает рассматривать тау (τ = 2π) как отдельную единицу измерения полного оборота. Давайте рассмотрим плюсы и минусы каждого из этих подходов:
| Подход | Преимущества | Недостатки |
|---|---|---|
| Традиционный (π) | Широко известен Имеет историческую основу Применяется в большинстве учебных материалов | Требует дополнительных вычислений Менее интуитивен для начинающих |
| Современный (τ) | Более естественен для восприятия Упрощает многие формулы Лучше отражает физическую суть | Меньшая распространенность Отсутствие в старых источниках |
Евгений Игоревич Жуков отмечает: «Переход на использование τ особенно полезен при обучении студентов, так как они быстрее усваивают материал и реже допускают ошибки в расчетах». Тем не менее, между сторонниками различных подходов существует ряд разногласий. Традиционалисты утверждают, что изменение устоявшейся системы может вызвать путаницу, особенно в междисциплинарных проектах. С другой стороны, прогрессивно настроенные исследователи показывают, как применение τ может оптимизировать множество вычислительных процессов. Например, при расчете параметров гармонического осциллятора использование τ позволяет сразу увидеть связь между периодом и угловой частотой без необходимости дополнительного умножения на 2. Это особенно важно при работе с многокомпонентными системами. Выбор подхода часто зависит от конкретной задачи. Например, в традиционных областях, таких как астрономия, по-прежнему предпочитают классический вариант, тогда как в новых направлениях, связанных с цифровыми технологиями, наблюдается тенденция к переходу на τ.
- Как выбрать подходящий метод?
- Как избежать ошибок при переходе между системами?
- Как адаптировать существующие алгоритмы для работы с τ?
Ответы на эти вопросы требуют глубокого понимания как математической сути проблемы, так и практических аспектов ее реализации.
Распространенные ошибки и способы их предотвращения
При использовании константы 2 пи часто возникают распространенные ошибки, которые могут значительно повлиять на точность расчетов. Одной из наиболее частых проблем является неправильное округление значения. Последние исследования (2025 год) показывают, что даже небольшое усечение числа может привести к накоплению ошибок в сложных вычислениях. Основные ошибки можно разделить на следующие категории:
- Применение недостаточной точности в расчетах
- Неправильный перевод единиц измерения
- Ошибки при переходе между градусами и радианами
- Неверное использование периодических свойств функций
Артём Викторович Озеров отмечает: «Крайне важно уделять внимание точности расчетов при работе с высокочастотными процессами. Даже малейшая погрешность может вызвать значительные отклонения в итоговых результатах». Евгений Игоревич Жуков добавляет: «Распространенной ошибкой является путаница понятий периода и частоты при использовании 2 пи. Это особенно критично в задачах, связанных с обработкой сигналов». Чтобы избежать этих проблем, рекомендуется придерживаться простых правил:
- Использовать максимально возможную точность в расчетах
- Дважды проверять единицы измерения
- Применять проверенные библиотеки математических функций
- Создавать тестовые случаи для проверки результатов
| Ошибка | Причина | Способ предотвращения |
|---|---|---|
| Накопление погрешности | Недостаточная точность | Использование double precision |
| Неверные единицы | Ошибка перевода | Автоматизация конвертации |
| Сдвиг фаз | Неправильное округление | Контроль промежуточных результатов |
Следует отметить, что современные программные решения часто предлагают встроенные механизмы защиты от распространенных ошибок. Тем не менее, нельзя полностью полагаться на них — важно понимать основные принципы работы с 2 пи.
Вопросы и ответы по теме 2 пи
Рассмотрим ключевые вопросы, которые могут возникнуть при использовании константы 2π:
- Как установить необходимую точность для расчетов? В большинстве случаев для практических задач достаточно 15-16 знаков после запятой. Однако в ситуациях, требующих высокой точности, может понадобиться большее количество знаков.
- Почему некоторые специалисты предпочитают τ вместо 2π? Константа τ более интуитивно понятна для многих физических процессов, так как она соответствует полному обороту, что упрощает восприятие формул.
- Как избежать ошибок при переводе между градусами и радианами? Рекомендуется использовать автоматизированные функции для преобразования и всегда указывать единицы измерения в расчетах.
Рассмотрим конкретный случай: при моделировании движения спутника произошла ошибка в расчете орбитальной скорости из-за использования неточного значения 2π. Решение заключалось в повышении точности константы и внедрении системы автоматической проверки результатов. Артём Викторович Озеров подчеркивает: «Крайне важно быть внимательным при работе с обратными тригонометрическими функциями, так как ошибки могут привести к значительным отклонениям в итогах». Также следует учитывать нестандартные ситуации, например, работу с очень большими или малыми углами, где традиционные методы могут давать неточные результаты. В таких случаях рекомендуется применять специальные алгоритмы для компенсации погрешностей.
Заключение и практические рекомендации
Подведем ключевые выводы: константа 2 пи является основополагающим значением, которое имеет важное значение в различных сферах науки и техники. От точности ее применения зависят результаты расчетов в таких областях, как физика, инженерия, компьютерная графика и многих других. Для эффективного использования 2 пи в практических задачах стоит учитывать следующие рекомендации:
- Обеспечивать необходимую точность при проведении вычислений
- Тщательно следить за единицами измерения
- Использовать проверенные методы расчетов
- Внедрять системы автоматической проверки результатов
Если вы столкнулись с задачей, требующей точных расчетов с применением 2 пи, и испытываете трудности в их выполнении, рекомендуется обратиться за более подробной консультацией к специалистам в области прикладной математики или инженерных расчетов.
Исторический контекст и развитие концепции 2 пи
Концепция числа 2π (двойное пи) имеет глубокие исторические корни, уходящие в древность. Пи, обозначаемое греческой буквой π, представляет собой отношение длины окружности к её диаметру и является иррациональным числом, приблизительно равным 3.14159. Однако, когда мы говорим о 2π, мы рассматриваем не только длину окружности, но и её полное окружение, что имеет важное значение в различных областях науки и математики.
Исторически, первые упоминания о числе π можно найти в работах древних цивилизаций, таких как египтяне и вавилоняне, которые использовали приближенные значения для расчётов, связанных с кругами. Однако именно в греческой математике, особенно в трудах Архимеда, началось более глубокое изучение этого числа. Архимед, используя метод исчерпывания, смог определить, что π находится между 3 1/7 и 3 10/71, что стало важным шагом в понимании этого математического константа.
С течением времени, математики различных эпох продолжали исследовать свойства π и его применения. В XVI веке, с развитием тригонометрии, число 2π стало особенно важным, так как оно связано с угловыми измерениями. В тригонометрии 2π радиан соответствует полному обороту вокруг круга, что делает его ключевым элементом в изучении периодических функций, таких как синус и косинус.
В XVIII веке, с работами таких математиков, как Леонард Эйлер, концепция 2π начала активно использоваться в различных областях, включая физику и инженерию. Эйлер ввёл формулу, связывающую экспоненциальные функции с тригонометрическими, известную как формула Эйлера: e^(iθ) = cos(θ) + i*sin(θ). В этой формуле 2π играет важную роль, так как при θ = 2π мы получаем полный круг на комплексной плоскости.
В XX веке число 2π стало неотъемлемой частью многих научных дисциплин, включая квантовую механику, теорию относительности и статистику. Например, в квантовой механике 2π появляется в уравнении Шрёдингера, а в статистике — в формуле для нормального распределения. Это подчеркивает универсальность и важность 2π в математике и науке.
Таким образом, исторический контекст и развитие концепции 2π демонстрируют, как это число прошло путь от простых геометрических наблюдений до сложных математических и физических теорий, становясь важным инструментом в понимании мира вокруг нас.
Вопрос-ответ
Какова роль числа 2π в математике и физике?
Число 2π часто используется в математике и физике для описания круговых и периодических явлений. Например, оно появляется в формулах для вычисления длины окружности (L = 2πr) и в уравнениях, связанных с волнами и колебаниями, таких как синусоидальные функции.
Почему 2π считается важным в тригонометрии?
В тригонометрии 2π соответствует полному обороту в круге, что делает его ключевым элементом для определения периодичности тригонометрических функций. Например, синус и косинус имеют период 2π, что означает, что их значения повторяются каждые 2π радиан.
Как 2π связано с комплексными числами?
Число 2π играет важную роль в комплексных числах через формулу Эйлера, которая утверждает, что e^(iθ) = cos(θ) + i*sin(θ). При θ = 2π эта формула показывает, что e^(i*2π) = 1, что иллюстрирует связь между экспоненциальными и тригонометрическими функциями.
Советы
СОВЕТ №1
Изучите основные свойства числа π (пи) и его приближенные значения. Это поможет вам лучше понять, как 2π (два пи) связано с кругами и окружностями, а также с тригонометрией.
СОВЕТ №2
Попробуйте визуализировать 2π на графиках. Построение кругов и синусоидальных функций поможет вам увидеть, как это число используется в различных математических и физических контекстах.
СОВЕТ №3
Применяйте 2π в практических задачах, таких как вычисление длины окружности или площади круга. Это поможет вам лучше усвоить концепцию и увидеть её применение в реальной жизни.
СОВЕТ №4
Не забывайте о связи 2π с периодическими функциями. Изучите, как 2π влияет на период синусоидальных и косинусоидальных функций, чтобы углубить свои знания в тригонометрии.
Концепция числа 2π (двойное пи) имеет глубокие исторические корни, уходящие в древность. Пи, обозначаемое греческой буквой π, представляет собой отношение длины окружности к её диаметру и является иррациональным числом, приблизительно равным 3.14159. Однако, когда мы говорим о 2π, мы рассматриваем не только длину окружности, но и её полное окружение, что имеет важное значение в различных областях науки и математики.
Исторически, первые упоминания о числе π можно найти в работах древних цивилизаций, таких как египтяне и вавилоняне, которые использовали приближенные значения для расчётов, связанных с кругами. Однако именно в греческой математике, особенно в трудах Архимеда, началось более глубокое изучение этого числа. Архимед, используя метод исчерпывания, смог определить, что π находится между 3 1/7 и 3 10/71, что стало важным шагом в понимании этого математического константа.
С течением времени, математики различных эпох продолжали исследовать свойства π и его применения. В XVI веке, с развитием тригонометрии, число 2π стало особенно важным, так как оно связано с угловыми измерениями. В тригонометрии 2π радиан соответствует полному обороту вокруг круга, что делает его ключевым элементом в изучении периодических функций, таких как синус и косинус.
В XVIII веке, с работами таких математиков, как Леонард Эйлер, концепция 2π начала активно использоваться в различных областях, включая физику и инженерию. Эйлер ввёл формулу, связывающую экспоненциальные функции с тригонометрическими, известную как формула Эйлера: e^(iθ) = cos(θ) + i*sin(θ). В этой формуле 2π играет важную роль, так как при θ = 2π мы получаем полный круг на комплексной плоскости.
В XX веке число 2π стало неотъемлемой частью многих научных дисциплин, включая квантовую механику, теорию относительности и статистику. Например, в квантовой механике 2π появляется в уравнении Шрёдингера, а в статистике — в формуле для нормального распределения. Это подчеркивает универсальность и важность 2π в математике и науке.
Таким образом, исторический контекст и развитие концепции 2π демонстрируют, как это число прошло путь от простых геометрических наблюдений до сложных математических и физических теорий, становясь важным инструментом в понимании мира вокруг нас.