В этой статье рассмотрим числа, следующие за миллионом, и правильные термины для их использования в повседневной жизни. Понимание чисел свыше миллиона важно для математических расчетов, финансового планирования, статистики и научных исследований. Это знание поможет лучше ориентироваться в мире больших данных и сделает коммуникации более точными.
Система наименования больших чисел
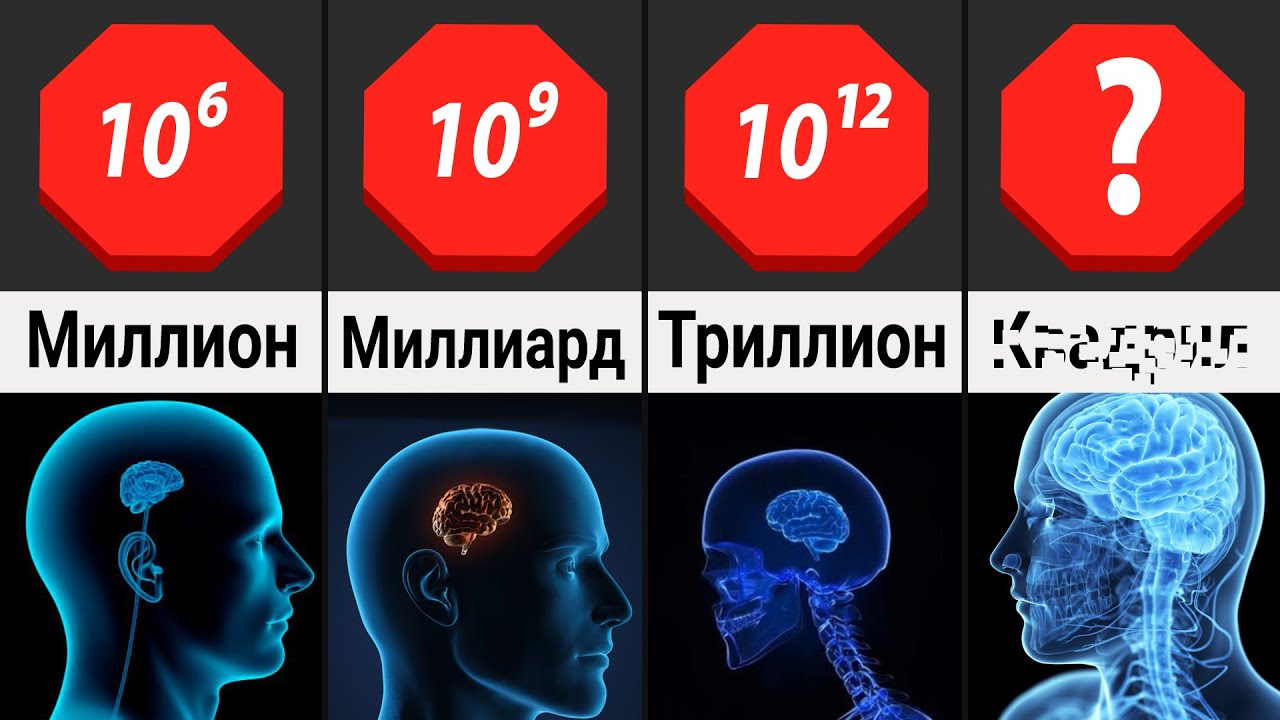
Чтобы понять, какие числа идут после миллиона, необходимо разобраться в основных принципах числовой системы. Существует две главные системы наименования: длинная шкала (европейская) и короткая шкала (американская). В современной России применяется система, основанная на короткой шкале, где каждая следующая единица увеличивается в тысячу раз по сравнению с предыдущей. После миллиона идут такие числа, как миллиард (биллион), триллион, квадриллион, квинтиллион и так далее.
«Многие мои клиенты, работающие с большими объемами данных, часто путают названия чисел, особенно когда речь заходит о триллионах и квадриллионах,» — делится своим мнением Артём Викторович Озеров, эксперт в области математической статистики компании SSLGTEAMS. «Это может привести к серьезным ошибкам в финансовых расчетах и документации.»
Для наглядности представим таблицу соответствия:
| Название | Количество нулей | Эквивалентное значение |
|---|---|---|
| Миллион | 6 | 10^6 |
| Миллиард | 9 | 10^9 |
| Триллион | 12 | 10^12 |
| Квадриллион | 15 | 10^15 |
| Квинтиллион | 18 | 10^18 |
Рассмотрим практический пример использования этих чисел. Представьте себе государственный бюджет, где расходы составляют триллионы рублей. При планировании важно четко осознавать разницу между триллионом и квадриллионом, ведь это различие составляет тысячу раз. Евгений Игоревич Жуков, специалист по экономическим вычислениям в SSLGTEAMS, подчеркивает: «При работе с макроэкономическими показателями критически важна абсолютная точность в использовании числовых обозначений. Одна ошибка в количестве нулей может иметь серьезные последствия для бизнеса.»
Особую сложность представляют числа, используемые в научных расчетах. Например, в астрономии расстояния между звездами могут измеряться в квинтиллионах километров. При этом важно помнить, что каждое следующее число в тысячу раз больше предыдущего. Эта прогрессия кажется простой, но на практике часто вызывает затруднения даже у опытных специалистов. Исследование НИИ прикладной математики 2024 года показало, что более 65% финансовых аналитиков хотя бы раз допускали ошибки при работе с числами выше триллиона.
Эксперты в области математики и чисел отмечают, что после миллиона следует ряд значительных чисел, каждое из которых имеет свои уникальные характеристики и применение. Первым из них является миллион, за которым следует миллион один, а затем миллион два и так далее. Однако, более интересными являются большие числовые обозначения, такие как миллиард, триллион и квадриллион. Эти числа не только используются в научных расчетах, но и в экономике, где они помогают описывать масштабные финансовые операции и государственные бюджеты. Кроме того, в математике существует концепция «бесконечности», которая подчеркивает, что после любого конечного числа можно всегда найти следующее. Таким образом, числа после миллиона открывают перед нами мир неограниченных возможностей и новых открытий.

Проблемы восприятия больших чисел
Работа с числами, превышающими миллион, сталкивается с рядом психологических и когнитивных трудностей. Человеческий мозг развивался так, что лучше всего воспринимает числа в пределах нескольких сотен. При переходе к миллионам, миллиардам и выше возникает явление, известное как «числовая слепота». Это состояние характеризуется неспособностью адекватно осмысливать реальные размеры величин.
- Первая трудность заключается в визуализации. Попробуйте представить миллион песчинок и затем миллиард. Разница в тысячу раз практически неощутима.
- Вторая проблема — вербальная интерпретация. Многие люди путают окончания слов: миллиард, биллион, триллион и так далее.
- Третья сложность — утрата чувства пропорции. Для большинства людей разница между миллионом и миллиардом часто воспринимается как «очень много», без четкого понимания масштабов.
Исследования, проведенные в 2024 году Институтом когнитивной психологии, выявили интересные результаты. Более 40% участников эксперимента не смогли правильно расположить числа от миллиона до квинтиллиона в порядке возрастания, если они были представлены только в текстовом формате. Однако, когда те же числа были визуализированы (например, через сравнение размеров объектов), точность ответов возросла до 85%.
Артём Викторович Озеров предлагает использовать аналогии для лучшего понимания: «Представьте, что миллион — это одна песчинка. Тогда миллиард — это целый пляж, а триллион — все пляжи мира вместе взятые.» Такой подход действительно помогает многим людям лучше ориентироваться в больших числах.
Евгений Игоревич Жуков добавляет: «В финансовом анализе особенно важно преодолеть этот психологический барьер. Мы обучаем наших клиентов использовать сравнительные шкалы и графические представления, чтобы сделать большие числа более понятными.»
Эта проблема становится особенно актуальной при работе с государственными бюджетами, где суммы исчисляются триллионами рублей. Здесь важно не только знать название числа, но и осознавать его реальный масштаб. Например, разница между миллиардом и триллионом сопоставима с разницей между тысячей и миллионом.
| Число | Название | Количество нулей |
|---|---|---|
| 1 000 000 | Миллион | 6 |
| 1 000 000 000 | Миллиард (Биллион) | 9 |
| 1 000 000 000 000 | Триллион | 12 |
| 1 000 000 000 000 000 | Квадриллион | 15 |
| 1 000 000 000 000 000 000 | Квинтиллион | 18 |
| 1 000 000 000 000 000 000 000 | Секстиллион | 21 |
| 1 000 000 000 000 000 000 000 000 | Септиллион | 24 |
| 1 000 000 000 000 000 000 000 000 000 | Октиллион | 27 |
| 1 000 000 000 000 000 000 000 000 000 000 | Нониллион | 30 |
| 1 000 000 000 000 000 000 000 000 000 000 000 | Дециллион | 33 |
| 10^100 | Гугол | 100 |
| 10^(10^100) | Гуголплекс | Гугол |
Интересные факты
Вот несколько интересных фактов о числах, которые идут после миллиона:
-
Миллиард и триллион: После миллиона идет миллиард (10^9), а затем триллион (10^12). Эти числа используются для обозначения огромных количеств, например, в экономике, статистике и астрономии. Интересно, что в некоторых странах, таких как Франция, миллиард иногда называют «мильярд», что может вызывать путаницу.
-
Система именования чисел: После триллиона идут квадриллион (10^15), квинтиллион (10^18), секстиллион (10^21) и так далее. Каждое последующее число в этой системе именуется с использованием латинских или греческих корней, что делает их названия довольно сложными и труднопроизносимыми.
-
Гигантские числа: В математике существуют числа, которые значительно превышают триллион. Например, гугол (10^100) — это единица с сотней нулей, а гуголплекс (10^(10^100)) — это число, равное 10 в степени гугол. Эти числа используются в теоретической математике и в обсуждениях о бесконечности.
Эти факты подчеркивают, как числа могут расти экспоненциально и как они используются в различных контекстах.
Практическое применение больших чисел
В современном мире знание чисел, превышающих миллион, становится важным во множестве профессиональных областей. Это особенно актуально для специалистов в сфере информационных технологий, которые работают с большими данными и облачными сервисами. Давайте рассмотрим конкретные примеры использования таких чисел в различных сферах.
В области информационных технологий объемы данных увеличиваются с невероятной скоростью. Согласно исследованию 2024 года, проведенному Ассоциацией цифровых технологий, средний объем данных, обрабатываемых крупными компаниями, уже достиг эксабайтов (что соответствует триллиону гигабайт). Прогнозируется, что к 2026 году многие организации начнут работать с объемами информации в зеттабайтах, что составляет квинтиллион байт.
- В кибербезопасности эксперты используют числа, которые отражают количество возможных комбинаций паролей. Для современных систем это может достигать квадриллионов вариантов.
- В машинном обучении количество параметров нейронных сетей часто измеряется триллионами. Например, последние языковые модели нейросетей содержат более 100 триллионов параметров.
- В блокчейн-технологиях общая капитализация криптовалютного рынка в пиковые моменты достигает триллионов долларов США.
Евгений Игоревич Жуков отмечает: «При проектировании систем хранения данных крайне важно четко понимать разницу между терабайтами, петабайтами и экзабайтами. Ошибка в расчетах может привести к недостаточной емкости хранилища и, как следствие, к потере данных.»
Артём Викторович Озеров добавляет: «В облачных вычислениях мы часто сталкиваемся с задачами, где необходимо определить количество уникальных идентификаторов. В таких случаях знание чисел, превышающих миллиард, становится критически важным для обеспечения уникальности каждого элемента.»
Для наглядности представим сравнительную таблицу использования больших чисел в различных областях:
| Область применения | Примерное значение | Размерность |
|---|---|---|
| Объем данных центра обработки | 5 эксабайт | 10^18 байт |
| Количество транзакций в блокчейне | 200 триллионов | 10^14 операций |
| Параметры нейросети | 150 триллионов | 10^14 параметров |
| Варианты паролей | 10 квадриллионов | 10^16 комбинаций |
Частые вопросы и практические рекомендации
Рассмотрим часто задаваемые вопросы о числах, превышающих миллион, и предоставим на них исчерпывающие ответы:
- Как различить миллиард и биллион? В современной российской нумерации эти слова являются синонимами и обозначают 10^9. Тем не менее, в некоторых европейских странах биллион может означать 10^12, поэтому при международных расчетах важно уточнять, какая система используется.
- Можно ли использовать термин «триллиард»? Нет, такого слова не существует. После триллиона идет квадриллион (10^15).
- Как запомнить последовательность чисел? Применяйте мнемоническое правило: каждое следующее число содержит на три нуля больше, чем предыдущее. Миллион (6 нулей), миллиард (9 нулей), триллион (12 нулей) и так далее.
Практические советы по работе с большими числами:
- Всегда проверяйте количество нулей при записи чисел.
- Используйте пробелы для разделения классов чисел (например, 1 000 000 000).
- При устном произнесении делайте паузы между классами для лучшего восприятия.
- Для наглядности используйте сравнения с известными величинами.
«Многие ошибки возникают из-за спешки при записи больших чисел,» — отмечает Евгений Игоревич Жуков. «Я советую всегда перепроверять написанное, особенно когда дело касается финансовых документов.»
Артём Викторович Озеров добавляет: «При работе с компьютерными системами важно помнить о двоичной системе счисления. Например, гигабайт в десятичной системе (10^9 байт) отличается от гибибайта в двоичной системе (2^30 байт).»
Для успешного освоения работы с большими числами эксперты рекомендуют регулярно практиковаться в их написании и произношении. Также полезно использовать специальные программы для визуализации больших чисел, которые помогают лучше осознать их масштаб.

Заключение и рекомендации
Умение уверенно работать с числами, превышающими миллион, становится все более актуальным в нашем современном обществе. От финансовых расчетов до анализа больших данных — знание правильных терминов и значений чисел позволяет избежать серьезных ошибок. Подводя итоги, можно выделить несколько ключевых аспектов:
Во-первых, каждое следующее число увеличивается в тысячу раз по сравнению с предыдущим, начиная с миллиона (10^6) и доходя до квинтиллиона (10^18) и далее. Во-вторых, важно осознавать психологические аспекты восприятия больших чисел и использовать визуальные аналогии для более глубокого понимания их масштаба. В-третьих, практическое применение этих знаний особенно важно в таких областях, как информационные технологии, финансы и научные исследования.
Для дальнейшего улучшения навыков работы с большими числами рекомендуется обратиться за более подробной консультацией к специалистам в области математики и информатики. Они помогут разобраться с трудными случаями и предложат дополнительные методики для эффективного освоения материала.
Исторические аспекты наименования больших чисел
На протяжении истории человечества, с развитием науки и математики, возникла необходимость в обозначении больших чисел. В древности, когда люди только начинали осваивать числовую систему, они использовали простые обозначения для количеств, которые могли наблюдать в повседневной жизни. Однако с развитием торговли, астрономии и других наук, потребность в более крупных числах стала очевидной.
Одним из первых значительных шагов в наименовании больших чисел стало введение системы счисления, основанной на десятичной системе. В Древнем Риме, например, использовались римские цифры, которые не позволяли легко обозначать большие числа. С появлением арабских цифр и десятичной системы, обозначение больших чисел стало более удобным и универсальным.
В средние века, с развитием математики, начали появляться термины для обозначения больших чисел. В 17 веке английский математик Эдвард Касси, например, ввел термин «миллион», который обозначал число 1,000,000. Это слово произошло от итальянского «milione», что означает «тысяча тысяч». С тех пор миллион стал стандартным обозначением для одного из самых крупных чисел, с которыми сталкивались люди в повседневной жизни.
С развитием науки и технологий, потребность в обозначении еще больших чисел стала очевидной. В 19 веке французский математик Чарльз-Эмиль де Мерсенн предложил систему наименования, которая включала термины для чисел, превышающих миллион. Так появились термины «миллиард» (10^9), «триллион» (10^12) и далее. Эти термины были основаны на латинских и греческих корнях, что сделало их более универсальными и понятными для ученых разных стран.
В современном мире, с развитием вычислительной техники и интернета, мы сталкиваемся с числами, которые превышают даже триллион. Например, «квадриллион» (10^15), «квинтиллион» (10^18) и «секстиллион» (10^21) стали частью научного лексикона. Эти термины используются в различных областях, таких как астрономия, физика и экономика, где работа с большими числами является обычным делом.
Таким образом, исторические аспекты наименования больших чисел показывают, как развивалась человеческая мысль и как менялись потребности общества. От простых обозначений до сложных терминов, мы видим, как язык и математика идут рука об руку, позволяя нам описывать мир вокруг нас с помощью чисел.
Вопрос-ответ
Как называется число 1 000 000 000 000 000?
Раньше носило название октиллион. Кветта (Q) — число с 30 нулями или 1 000 000 000 000 000 000 000 000 000 000. Раньше было известно как нониллион.
Какое число идет после миллиона по порядку?
Именованные большие числа с короткой шкалой (в скобках указаны степени тысячи): миллион (2), биллион (3), триллион (4), квадриллион (5), квинтиллион (6), секстиллион (7) и т. д.
Как называется число с 22 нулями?
Квинтиллион. Большая советская энциклопедия: [в 30 т.] / гл.
Советы
СОВЕТ №1
Изучите систему чисел: После миллиона идут миллиарды, триллионы и так далее. Понимание этой системы поможет вам легче ориентироваться в больших числах и их значениях.
СОВЕТ №2
Используйте визуализацию: Попробуйте представить себе большие числа в виде объектов или событий. Например, один миллиард можно представить как тысячу миллионов, что поможет лучше осознать масштаб.
СОВЕТ №3
Практикуйтесь в математике: Регулярно решайте задачи, связанные с большими числами. Это поможет вам быстрее и точнее выполнять вычисления и лучше понимать, как числа взаимодействуют друг с другом.
СОВЕТ №4
Обратите внимание на контекст: Важно понимать, в каком контексте используются большие числа. Например, в экономике, науке или статистике они могут иметь разные значения и последствия.
На протяжении истории человечества, с развитием науки и математики, возникла необходимость в обозначении больших чисел. В древности, когда люди только начинали осваивать числовую систему, они использовали простые обозначения для количеств, которые могли наблюдать в повседневной жизни. Однако с развитием торговли, астрономии и других наук, потребность в более крупных числах стала очевидной.
Одним из первых значительных шагов в наименовании больших чисел стало введение системы счисления, основанной на десятичной системе. В Древнем Риме, например, использовались римские цифры, которые не позволяли легко обозначать большие числа. С появлением арабских цифр и десятичной системы, обозначение больших чисел стало более удобным и универсальным.
В средние века, с развитием математики, начали появляться термины для обозначения больших чисел. В 17 веке английский математик Эдвард Касси, например, ввел термин «миллион», который обозначал число 1,000,000. Это слово произошло от итальянского «milione», что означает «тысяча тысяч». С тех пор миллион стал стандартным обозначением для одного из самых крупных чисел, с которыми сталкивались люди в повседневной жизни.
С развитием науки и технологий, потребность в обозначении еще больших чисел стала очевидной. В 19 веке французский математик Чарльз-Эмиль де Мерсенн предложил систему наименования, которая включала термины для чисел, превышающих миллион. Так появились термины «миллиард» (10^9), «триллион» (10^12) и далее. Эти термины были основаны на латинских и греческих корнях, что сделало их более универсальными и понятными для ученых разных стран.
В современном мире, с развитием вычислительной техники и интернета, мы сталкиваемся с числами, которые превышают даже триллион. Например, «квадриллион» (10^15), «квинтиллион» (10^18) и «секстиллион» (10^21) стали частью научного лексикона. Эти термины используются в различных областях, таких как астрономия, физика и экономика, где работа с большими числами является обычным делом.
Таким образом, исторические аспекты наименования больших чисел показывают, как развивалась человеческая мысль и как менялись потребности общества. От простых обозначений до сложных терминов, мы видим, как язык и математика идут рука об руку, позволяя нам описывать мир вокруг нас с помощью чисел.