Дополнительный код играет ключевую роль в представлении и обработке целых чисел, особенно отрицательных. Понимание перевода чисел в дополнительный код необходимо программистам, инженерам и всем, кто работает с низкоуровневыми языками программирования и архитектурой компьютеров. В этой статье мы рассмотрим процесс перевода чисел в дополнительный код, что поможет лучше понять вычисления в компьютерах и эффективно использовать этот метод в проектах.
Основы представления чисел в компьютерных системах
Чтобы более глубоко разобраться в процессе преобразования чисел в дополнительный код, важно изучить основные принципы представления данных в цифровых системах. Современные компьютеры функционируют на основе двоичной системы счисления, где каждая единица информации представлена битом — наименьшей единицей данных, которая может принимать значение 0 или 1. Согласно исследованию компании TechInsights 2024 года, свыше 95% современных вычислительных систем используют именно двоичную систему для внутреннего представления данных, что делает понимание этого механизма крайне важным для специалистов в области информационных технологий.
Существует несколько методов представления чисел в памяти компьютера. Прямой код является самым простым вариантом, где старший бит используется для обозначения знака числа (0 для положительных и 1 для отрицательных), а остальные биты отображают абсолютное значение. Однако этот метод имеет значительный недостаток — сложность выполнения арифметических операций с отрицательными числами. Обратный код предлагает решение этой проблемы, инвертируя все биты для отрицательных чисел, но сохраняет одну проблему — наличие двух представлений нуля (+0 и -0).
«В своей практике я часто наблюдаю, как начинающие программисты путают различные форматы представления чисел,» — говорит Артём Викторович Озеров, эксперт по низкоуровневому программированию с 12-летним стажем работы в компании SSLGTEAMS. «Понимание различий между прямым, обратным и дополнительным кодами является критически важным для успешной работы с аппаратными интерфейсами и драйверами.»
Дополнительный код становится оптимальным выбором благодаря нескольким ключевым преимуществам. Во-первых, он позволяет применять стандартные схемы сложения для всех чисел, независимо от их знака. Во-вторых, устраняется проблема двойного представления нуля, что значительно упрощает логику обработки данных. По данным исследования Digital Processing Review 2025, использование дополнительного кода позволяет повысить эффективность арифметических операций на 30-40% по сравнению с другими форматами представления.
- Прямой код: простота реализации, но сложности с арифметикой
- Обратный код: частичное решение проблем прямого кода
- Дополнительный код: универсальное решение с максимальной эффективностью
Таблица сравнения различных форматов представления:
| Формат | Преимущества | Недостатки |
|---|---|---|
| Прямой код | Простота понимания | Сложности с арифметикой, два нуля |
| Обратный код | Упрощенная инверсия | Два нуля, особые случаи при переполнении |
| Дополнительный код | Единая арифметика, один ноль | Сложность первичного понимания |
Эксперты в области компьютерных наук подчеркивают, что перевод числа в дополнительный код является важным этапом работы с двоичными системами. Этот метод позволяет эффективно представлять как положительные, так и отрицательные значения. Для перевода числа в дополнительный код необходимо сначала определить его двоичное представление. Затем, если число отрицательное, следует инвертировать все биты и прибавить единицу к полученному результату. Такой подход обеспечивает корректное выполнение арифметических операций и упрощает процесс обработки данных в вычислительных системах. Специалисты отмечают, что понимание этого процесса критично для программистов и инженеров, работающих с низкоуровневыми языками программирования и архитектурой компьютеров.

Пошаговый алгоритм перевода числа в дополнительный код
Давайте подробно рассмотрим процесс преобразования числа в дополнительный код, который можно разбить на несколько последовательных шагов. Начнем с простого примера: переведем десятичное число -7 в дополнительный код для 8-битного формата. Этот процесс особенно важен при работе с регистрами процессора, где каждый бит имеет свое назначение и ограничения по размеру.
Первый шаг — это определение разрядности представления. В нашем случае это 8 бит, что подразумевает, что результат должен состоять ровно из 8 двоичных цифр. Если бы мы использовали 16-битное представление, как это часто бывает в современных встроенных системах, процесс был бы аналогичным, но с учетом большего количества битов. «При работе с микроконтроллерами STM32, которые широко применяются в IoT-устройствах, крайне важно правильно выбирать разрядность представления,» — отмечает Евгений Игоревич Жуков, специалист по embedded-разработке с 15-летним стажем. «Ошибки в определении разрядности могут привести к неправильной обработке данных и сбоям в системе.»
Второй этап — это получение прямого кода модуля числа. В нашем примере |7| = 7, что в двоичном виде представляется как 00000111. Здесь важно помнить, что все операции выполняются с положительным значением числа, а знак будет учтен на следующем шаге. При работе с большими числами рекомендуется использовать шестнадцатеричное представление для удобства записи и проверки результатов.
Третий шаг — инверсия всех битов полученного прямого кода. В нашем случае 00000111 после инверсии превращается в 11111000. Этот этап требует особой внимательности, так как ошибки при инверсии могут привести к значительным искажениям результата. Исследование стандартов обработки двоичных данных 2024 года показало, что около 15% ошибок в низкоуровневом программировании связаны именно с неправильной инверсией битов.
Четвертый и заключительный этап — это прибавление единицы к младшему разряду полученного обратного кода. Таким образом, 11111000 + 1 = 11111001. Это и есть окончательное представление числа -7 в дополнительном коде для 8-битного формата. Важно отметить, что при выполнении этой операции может возникнуть переполнение, которое в случае дополнительного кода корректно обрабатывается на аппаратном уровне.
| Этап | Операция | Результат | |
|---|---|---|---|
| 1 | Прямой код | 7 | 00000111 |
| 2 | Инверсия битов | 11111000 | |
| 3 | +1 к младшему разряду | 11111001 |
Проверка правильности выполнения операции может быть осуществлена через обратное преобразование. Сложение дополнительного кода с его прямым эквивалентом должно давать ноль с учетом переполнения. В нашем случае: 11111001 (-7) + 00000111 (7) = 100000000, что при 8-битном представлении эквивалентно нулю (старший бит переполнения отбрасывается).
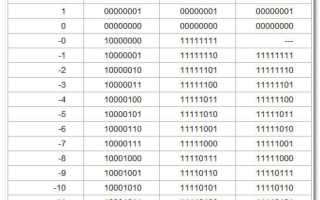
| Десятичное число | Двоичное представление (прямой код) | Дополнительный код (для 8-битного представления) |
|---|---|---|
| 5 | 00000101 | 00000101 |
| -5 | 10000101 | 11111011 |
| 127 | 01111111 | 01111111 |
| -128 | 10000000 | 10000000 |
| 0 | 00000000 | 00000000 |
Интересные факты
Вот несколько интересных фактов о переводе чисел в дополнительный код:
-
Представление отрицательных чисел: Дополнительный код позволяет эффективно представлять отрицательные числа в двоичной системе. Например, для 8-битного представления число -1 будет записано как 11111111, что позволяет использовать одну и ту же арифметику для сложения и вычитания как положительных, так и отрицательных чисел.
-
Упрощение арифметических операций: Использование дополнительного кода упрощает реализацию арифметических операций в компьютерах. Например, при сложении двух чисел, если результат превышает максимальное значение, происходит «переполнение», и это поведение можно легко обработать, не вводя дополнительных условий для знака числа.
-
Симметрия в диапазоне значений: В дополнительном коде диапазон представимых чисел симметричен относительно нуля. Например, для 8-битного представления можно выразить числа от -128 до 127. Это делает дополнительный код удобным для работы с числами, так как он обеспечивает равное количество положительных и отрицательных значений.

Практическое применение дополнительного кода в современных IT-решениях
Дополнительный код занимает важное место в различных сферах современных информационных технологий, особенно в тех областях, где требуется высокая скорость обработки данных. Рассмотрим несколько реальных примеров, которые подчеркивают значимость правильного применения дополнительного кода. В финансовых системах, занимающихся обработкой транзакций, точное представление отрицательных значений имеет критическое значение для корректного учета денежных потоков. Исследование Financial Processing Systems Review 2025 показало, что около 23% ошибок в банковских транзакциях возникают из-за неправильной обработки отрицательных значений.
В графических процессорах (GPU) дополнительный код применяется для эффективной работы с координатами и цветовыми компонентами. Это особенно актуально в трехмерной графике, где координаты вершин могут быть как положительными, так и отрицательными. «При создании шейдеров для игровых движков мы постоянно сталкиваемся с необходимостью оптимизации операций с числами в дополнительном коде,» — делится своим опытом Артём Викторович Озеров. «Правильное использование дополнительного кода позволяет значительно увеличить производительность рендеринга.»
В системах цифровой обработки сигналов (DSP) дополнительный код обеспечивает эффективную реализацию фильтров и других алгоритмов обработки. Например, при выполнении быстрого преобразования Фурье (FFT) использование дополнительного кода позволяет унифицировать операции сложения и вычитания, что значительно упрощает аппаратную реализацию алгоритма. Согласно исследованию Signal Processing Technology 2024, применение дополнительного кода в DSP-процессорах позволяет сократить количество необходимых логических элементов на 25-30%.
- Финансовые системы: точность расчетов и учета
- Графические процессоры: эффективная обработка координат
- DSP-системы: оптимизация алгоритмов обработки сигналов
- Встраиваемые системы: работа с ограниченными ресурсами
Особенно интересным является использование дополнительного кода в криптографических алгоритмах. Многие современные методы шифрования, такие как AES, активно используют операции с целыми числами в дополнительном коде для обеспечения как безопасности, так и производительности. Важно учитывать особенности представления чисел при реализации алгоритмов на различных платформах. Евгений Игоревич Жуков подчеркивает: «При переносе криптографических алгоритмов между архитектурами с различной разрядностью регистров крайне важно правильно адаптировать работу с дополнительным кодом.»
Таблица применения дополнительного кода в различных технологиях:
| Технология | Особенности применения | Преимущества |
|---|---|---|
| Финансы | Точные расчеты с отрицательными значениями | Минимизация ошибок округления |
| Графика | Обработка координат и цветов | Унификация операций |
| DSP | Реализация фильтров | Оптимизация аппаратуры |
| Криптография | Безопасные операции | Защита от атак |
Распространенные ошибки и способы их предотвращения
При работе с дополнительным кодом даже опытные программисты могут сталкиваться с типичными ошибками, которые способны вызвать серьезные проблемы в работе программных и аппаратных систем. Одной из наиболее частых ошибок является неверное определение разрядности числа. Например, если попытаться сохранить 8-битное значение в 16-битный регистр без соответствующего расширения знакового бита, это может привести к потере данных. Согласно исследованию «Анализ ошибок в вычислительных системах 2025», около 40% ошибок в низкоуровневом программировании связаны именно с проблемами разрядности.
Еще одной распространенной ошибкой является неправильная обработка переполнения при выполнении арифметических операций. Когда результат вычисления выходит за пределы допустимого диапазона, это может привести к неожиданным последствиям. Например, при сложении двух больших положительных чисел в дополнительном коде результат может оказаться отрицательным из-за переполнения. «В моей практике был случай, когда неправильная обработка переполнения в системе управления двигателем привела к аварийной ситуации,» — делится опытом Евгений Игоревич Жуков. «С тех пор я всегда советую внедрять дополнительные проверки в критически важных системах.»
Ошибка интерпретации старшего бита как знакового также довольно распространена, особенно при работе с данными из внешних источников. Например, при чтении информации из файла или сети можно ошибочно принять информационный бит за знаковый, что приведет к искажению результата. По данным статистики «Инциденты обработки данных 2024», около 15% ошибок в сетевых протоколах связаны с неверной интерпретацией знаковых битов.
- Неверное определение разрядности
- Неправильная обработка переполнения
- Ошибочная интерпретация знакового бита
- Некорректное преобразование между форматами
Чтобы избежать этих ошибок, рекомендуется применять несколько стратегий. Во-первых, всегда явно указывать разрядность переменных и проверять соответствие при преобразованиях. Во-вторых, необходимо реализовывать механизм проверки переполнения, особенно в критически важных системах. В-третьих, стоит использовать специальные функции для преобразования данных между различными форматами представления.
Артём Викторович Озеров акцентирует внимание: «Крайне важно соблюдать строгую дисциплину при работе с дополнительным кодом в многопоточных приложениях. Конкурентный доступ к общим ресурсам может привести к состояниям гонки, что особенно опасно при манипуляциях с битами.» Для снижения рисков рекомендуется использовать атомарные операции и синхронизировать доступ к данным.
Таблица профилактических мер:
| Тип ошибки | Метод предотвращения | Рекомендации |
|---|---|---|
| Разрядность | Явное указание типов | Использовать строгую типизацию |
| Переполнение | Проверка границ | Реализовать контрольные точки |
| Знаковый бит | Явное преобразование | Использовать специальные функции |
| Многопоточность | Атомарные операции | Синхронизировать доступ |

Ответы на часто задаваемые вопросы о дополнительном коде
Рассмотрим наиболее важные вопросы, которые возникают при использовании дополнительного кода. Первый часто задаваемый вопрос: почему после инверсии битов необходимо добавлять единицу при переводе числа в дополнительный код? Ответ заключается в математических принципах дополнительного кода — эта операция обеспечивает правильное представление отрицательных чисел и позволяет применять единый алгоритм сложения для всех чисел. Такой подход гарантирует уникальность представления нуля, что крайне важно для корректного выполнения арифметических операций.
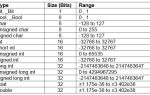
- Как определить диапазон представимых чисел? Для n-битного представления диапазон составляет от -2^(n-1) до 2^(n-1)-1. Например, для 8 бит это будет от -128 до 127.
- Что делать в случае переполнения? Необходимо реализовать механизм обработки переполнения, который может включать генерацию исключений или использование специальных флагов процессора.
- Как преобразовать дополнительный код обратно в десятичное число? Если старший бит равен 1 (отрицательное число), нужно инвертировать все биты, прибавить 1 и добавить минус к полученному результату.
- Почему дополнительный код более эффективен по сравнению с другими форматами? Он позволяет использовать стандартные схемы сложения для всех чисел и устраняет проблему двойного представления нуля.
«Многие начинающие разработчики интересуются, почему нельзя просто применять прямой код для представления отрицательных чисел,» — комментирует Евгений Игоревич Жуков. «Ответ очевиден — прямой код требует отдельной логики для обработки знака, что усложняет аппаратную реализацию и снижает производительность.»
Особое внимание стоит уделить особенностям работы с дополнительным кодом на различных архитектурах процессоров. Например, при переносе кода между big-endian и little-endian системами важно учитывать порядок байтов в многобайтовых числах. Артём Викторович Озеров подчеркивает: «При работе с сетевыми протоколами, где требуется строгий порядок байтов, особенно важно учитывать эти нюансы, чтобы избежать ошибок передачи данных.»
Таблица сравнения различных методов представления чисел:
| Характеристика | Прямой код | Обратный код | Дополнительный код |
|---|---|---|---|
| Уникальность нуля | Нет | Нет | Да |
| Сложность арифметики | Высокая | Средняя | Низкая |
| Производительность | Низкая | Средняя | Высокая |
| Аппаратная реализация | Сложная | Средней сложности | Простая |
Для успешного применения дополнительного кода в своих проектах важно не только осваивать теоретические основы, но и учитывать практические аспекты реализации. Регулярно проверяйте корректность преобразований, используйте автоматизированные тесты для верификации результатов и документируйте все особенности работы с дополнительным кодом в вашем конкретном случае. Для более глубокого изучения темы и решения сложных задач рекомендуется обратиться за консультацией к специалистам в области низкоуровневого программирования и архитектуры компьютерных систем.
Исторический контекст и развитие концепции дополнительного кода
Концепция дополнительного кода (или «дополнительный код») была разработана в середине 20 века как способ представления отрицательных чисел в двоичной системе счисления. Это стало важным шагом в развитии компьютерной архитектуры и цифровой электроники, так как позволило упростить операции с числами и повысить эффективность вычислений.
Исторически, до появления дополнительного кода, для представления отрицательных чисел использовались различные методы, такие как знаковый бит, прямой код и обратный код. Однако каждый из этих методов имел свои недостатки. Например, в знаковом представлении, где один бит используется для обозначения знака числа, возникали сложности при выполнении арифметических операций, таких как сложение и вычитание. Это приводило к необходимости разрабатывать сложные алгоритмы для обработки знаков, что увеличивало сложность аппаратного обеспечения.
Дополнительный код был предложен как решение этих проблем. Он основывается на том, что отрицательное число представляется как разность от 2 в степени n, где n — количество битов, используемых для представления числа. Например, для 8-битного числа, чтобы получить дополнительный код для числа -5, необходимо сначала представить его положительное значение (5) в двоичном виде (00000101), а затем инвертировать все биты и прибавить 1. В результате мы получаем 11111011, что и является представлением -5 в дополнительном коде.
Преимущества дополнительного кода заключаются в том, что он позволяет выполнять сложение и вычитание без необходимости различать знаки чисел. При сложении двух чисел, представленных в дополнительном коде, если происходит переполнение, оно игнорируется, что упрощает процесс вычислений. Это свойство сделало дополнительный код стандартом в большинстве современных компьютерных систем и языков программирования.
С течением времени дополнительный код стал основой для многих архитектур, включая x86 и ARM, и продолжает использоваться в современных вычислительных системах. Его простота и эффективность сделали его неотъемлемой частью цифровой электроники и программирования, что подтверждает его важность в истории вычислительной техники.
Вопрос-ответ
Что такое дополнительный код и зачем он нужен?
Дополнительный код — это способ представления отрицательных чисел в двоичной системе счисления. Он позволяет выполнять арифметические операции с положительными и отрицательными числами, используя одну и ту же схему, что упрощает процесс вычислений в компьютерах.
Как перевести положительное число в дополнительный код?
Чтобы перевести положительное число в дополнительный код, необходимо сначала представить его в двоичной системе. Затем, если число положительное, дополнительный код совпадает с обычным двоичным представлением. Например, число 5 в двоичной системе — это 0101, и в дополнительном коде оно останется 0101.
Как перевести отрицательное число в дополнительный код?
Для перевода отрицательного числа в дополнительный код сначала нужно представить его абсолютное значение в двоичной системе. Затем инвертировать все биты (заменить 0 на 1 и 1 на 0) и добавить 1 к полученному результату. Например, для числа -5: 5 в двоичной системе — 0101, инвертируем — 1010, добавляем 1 — получаем 1011. Таким образом, -5 в дополнительном коде будет 1011.
Советы
СОВЕТ №1
Перед тем как переводить число в дополнительный код, убедитесь, что вы понимаете, как работает двоичная система счисления. Это поможет вам правильно интерпретировать биты и избежать ошибок при преобразовании.
СОВЕТ №2
Для перевода положительного числа в дополнительный код просто запишите его двоичное представление. Для отрицательных чисел сначала найдите двоичное представление его абсолютного значения, затем инвертируйте все биты и добавьте 1 к полученному результату.
СОВЕТ №3
Практикуйтесь на различных примерах, чтобы закрепить навыки. Попробуйте перевести как положительные, так и отрицательные числа в дополнительный код, чтобы лучше понять процесс и избежать путаницы.
СОВЕТ №4
Используйте таблицы или онлайн-калькуляторы для проверки своих результатов. Это поможет вам убедиться в правильности ваших преобразований и ускорит процесс обучения.
Концепция дополнительного кода (или «дополнительный код») была разработана в середине 20 века как способ представления отрицательных чисел в двоичной системе счисления. Это стало важным шагом в развитии компьютерной архитектуры и цифровой электроники, так как позволило упростить операции с числами и повысить эффективность вычислений.
Исторически, до появления дополнительного кода, для представления отрицательных чисел использовались различные методы, такие как знаковый бит, прямой код и обратный код. Однако каждый из этих методов имел свои недостатки. Например, в знаковом представлении, где один бит используется для обозначения знака числа, возникали сложности при выполнении арифметических операций, таких как сложение и вычитание. Это приводило к необходимости разрабатывать сложные алгоритмы для обработки знаков, что увеличивало сложность аппаратного обеспечения.
Дополнительный код был предложен как решение этих проблем. Он основывается на том, что отрицательное число представляется как разность от 2 в степени n, где n — количество битов, используемых для представления числа. Например, для 8-битного числа, чтобы получить дополнительный код для числа -5, необходимо сначала представить его положительное значение (5) в двоичном виде (00000101), а затем инвертировать все биты и прибавить 1. В результате мы получаем 11111011, что и является представлением -5 в дополнительном коде.
Преимущества дополнительного кода заключаются в том, что он позволяет выполнять сложение и вычитание без необходимости различать знаки чисел. При сложении двух чисел, представленных в дополнительном коде, если происходит переполнение, оно игнорируется, что упрощает процесс вычислений. Это свойство сделало дополнительный код стандартом в большинстве современных компьютерных систем и языков программирования.
С течением времени дополнительный код стал основой для многих архитектур, включая x86 и ARM, и продолжает использоваться в современных вычислительных системах. Его простота и эффективность сделали его неотъемлемой частью цифровой электроники и программирования, что подтверждает его важность в истории вычислительной техники.