В цифровую эпоху умение переводить числа в шестнадцатеричную систему стало важным навыком для программистов и IT-специалистов. Шестнадцатеричная система широко используется в программировании, особенно при работе с цветами в веб-дизайне, адресами в памяти и кодами ошибок. В этой статье рассмотрим простые и эффективные методы перевода чисел в шестнадцатеричную систему, что поможет лучше понимать и работать с данными в информационных технологиях.
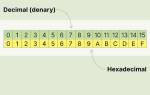
Основные принципы шестнадцатеричной системы счисления
Перевод чисел в шестнадцатеричную систему требует знания её основных принципов. Шестнадцатеричная система — это позиционная система счисления с основанием 16, что подразумевает использование шестнадцати уникальных символов для представления чисел. Эти символы включают в себя обычные десятичные цифры от 0 до 9, а также буквы A, B, C, D, E и F, которые обозначают значения от 10 до 15 соответственно. Каждая позиция в числе имеет вес, равный степени числа 16, начиная с нулевой степени справа.
Чтобы лучше понять структуру шестнадцатеричной системы, обратим внимание на следующую таблицу:
| Позиция | 3 | 2 | 1 | 0 |
| Вес | 4096 (16³) | 256 (16²) | 16 (16¹) | 1 (16⁰) |
Артём Викторович Озеров акцентирует внимание на важности осознания весовых коэффициентов: «Многие новички совершают ошибки именно из-за неверного учета весов позиций при переводе чисел». Эта система широко используется в компьютерных технологиях благодаря своей компактности и удобству представления двоичных данных. Например, один шестнадцатеричный символ может заменить четыре двоичных бита, что значительно облегчает чтение и запись больших двоичных чисел.
Евгений Игоревич Жуков подчеркивает практическое применение этой системы: «В процессе разработки встроенных систем мы постоянно взаимодействуем с регистрами микроконтроллеров, где шестнадцатеричная запись становится незаменимым инструментом». Также стоит отметить, что шестнадцатеричная система имеет прямую связь с двоичной — каждая шестнадцатеричная цифра соответствует четырем двоичным битам, что делает конвертацию между этими системами особенно простой и быстрой.
У данной системы есть ряд преимуществ по сравнению с другими системами счисления: она более компактна, чем двоичная, легче воспринимается человеком, чем длинные последовательности нулей и единиц, и при этом сохраняет прямую связь с внутренним представлением данных в компьютере. Эти характеристики сделали шестнадцатеричную систему стандартом во многих областях информационных технологий, включая программирование, сетевые протоколы и криптографию.
Эксперты в области программирования и математики подчеркивают, что перевод числа в шестнадцатеричную систему счисления является важным навыком для разработчиков и инженеров. Процесс начинается с деления числа на 16, при этом остаток от деления определяет последнюю цифру в шестнадцатеричном представлении. Если остаток больше 9, он заменяется на соответствующую букву от A до F. Затем деление продолжается с целой частью результата, пока она не станет равной нулю. Полученные остатки записываются в обратном порядке. Эксперты отмечают, что понимание этой процедуры не только облегчает работу с различными системами счисления, но и помогает лучше осваивать программирование и компьютерные науки в целом.
https://youtube.com/watch?v=AkXHkwVCcRU
Методы перевода чисел в шестнадцатеричную систему
Существует несколько ключевых способов перевода чисел в шестнадцатеричную систему, каждый из которых обладает своими особенностями и применяется в различных ситуациях. Первый способ заключается в последовательном делении исходного десятичного числа на 16 до тех пор, пока результат деления не станет меньше 16. Остатки от каждого деления записываются в обратном порядке и преобразуются в соответствующие символы шестнадцатеричной системы. Например, при переводе числа 3789: 3789 ÷ 16 = 236 (остаток 13=D), 236 ÷ 16 = 14 (остаток 12=C), 14 = E, что в итоге дает ECD₁₆.
Второй способ основан на разложении числа по степеням 16. Сначала определяется наибольшая степень 16, которая меньше или равна исходному числу, затем вычисляется коэффициент для этой степени, и процесс повторяется для остатка. Этот метод особенно полезен при работе с большими числами. Например, число 43875 включает 1×16³=4096, остаток 291 после вычитания; 11×16²=2816, остаток 10; в результате получаем AB2A₁₆.
Третий способ использует промежуточную двоичную систему. Сначала десятичное число переводится в двоичную систему, а затем разбивается на группы по 4 бита (тетрады), каждая из которых преобразуется в соответствующую шестнадцатеричную цифру. Этот метод особенно эффективен для работы с данными в компьютерной среде. Например, число 185 в двоичной системе представляется как 10111001₂, что разбивается на 1011(B) и 1001(9), в результате чего получается B9₁₆.
| Метод | Преимущества | Недостатки | Рекомендуемые случаи использования |
|---|---|---|---|
| Деление на 16 | Легкость реализации | Многочисленные вычисления | Небольшие числа |
| Степенное разложение | Высокая точность расчетов | Сложности с большими числами | Научные вычисления |
| Через двоичную систему | Автоматизация процесса | Необходимость промежуточных преобразований | Компьютерные технологии |
Выбор метода зависит от конкретной задачи и контекста применения. Артём Викторович Озеров подчеркивает: «В реальных проектах часто используются различные методы в зависимости от ситуации — например, для отладки применяются табличные преобразования, а для автоматизации — алгоритмические подходы».
| Десятичное число | Шестнадцатеричное представление | Пример деления на 16 (остаток) |
|---|---|---|
| 0 | 0 | 0 / 16 = 0 (0) |
| 1 | 1 | 1 / 16 = 0 (1) |
| 2 | 2 | 2 / 16 = 0 (2) |
| 3 | 3 | 3 / 16 = 0 (3) |
| 4 | 4 | 4 / 16 = 0 (4) |
| 5 | 5 | 5 / 16 = 0 (5) |
| 6 | 6 | 6 / 16 = 0 (6) |
| 7 | 7 | 7 / 16 = 0 (7) |
| 8 | 8 | 8 / 16 = 0 (8) |
| 9 | 9 | 9 / 16 = 0 (9) |
| 10 | A | 10 / 16 = 0 (10) |
| 11 | B | 11 / 16 = 0 (11) |
| 12 | C | 12 / 16 = 0 (12) |
| 13 | D | 13 / 16 = 0 (13) |
| 14 | E | 14 / 16 = 0 (14) |
| 15 | F | 15 / 16 = 0 (15) |
| 16 | 10 | 16 / 16 = 1 (0) -> 1 / 16 = 0 (1) |
| 17 | 11 | 17 / 16 = 1 (1) -> 1 / 16 = 0 (1) |
| 31 | 1F | 31 / 16 = 1 (15) -> 1 / 16 = 0 (1) |
| 255 | FF | 255 / 16 = 15 (15) -> 15 / 16 = 0 (15) |
Интересные факты
Вот несколько интересных фактов о переводе чисел в шестнадцатеричную систему:
-
Шестнадцатеричная система и байты: Шестнадцатеричная система (основание 16) широко используется в программировании и компьютерных науках, поскольку один байт (8 бит) можно удобно представить двумя шестнадцатеричными цифрами. Это упрощает чтение и запись двоичных данных, так как каждая шестнадцатеричная цифра соответствует 4 битам.
-
Использование букв: В шестнадцатеричной системе используются не только цифры от 0 до 9, но и буквы от A до F, которые представляют значения от 10 до 15. Это позволяет компактно представлять большие числа, что особенно полезно в контексте адресации памяти и цветовых кодов в веб-дизайне (например, #FF5733).
-
Перевод из десятичной системы: Для перевода числа из десятичной системы в шестнадцатеричную, можно использовать метод деления на 16. Делите число на 16, записывая остатки, и продолжайте делить целую часть результата, пока она не станет равной нулю. Остатки, записанные в обратном порядке, и будут шестнадцатеричным представлением числа.
https://youtube.com/watch?v=V7ukC1tdcvY
Пошаговая инструкция перевода чисел
Рассмотрим детальный алгоритм преобразования десятичного числа в шестнадцатеричную систему на примере числа 12345, выполняя все шаги последовательно. Начнем с деления числа на 16: 12345 ÷ 16 = 771 с остатком 9. Этот остаток мы записываем как младший разряд будущего шестнадцатеричного числа. Далее, берем целую часть результата (771) и снова делим на 16: 771 ÷ 16 = 48 с остатком 3. Этот остаток станет следующим разрядом. Продолжаем: 48 ÷ 16 = 3 с остатком 0, и, наконец, 3 ÷ 16 = 0 с остатком 3. Записывая остатки в обратном порядке, мы получаем результат 3039₁₆.
- Шаг 1: Определить начальное десятичное число
- Шаг 2: Провести целочисленное деление на 16
- Шаг 3: Записать остаток от деления
- Шаг 4: Повторить деление с целой частью результата
- Шаг 5: Продолжать процесс до тех пор, пока частное не станет нулем
- Шаг 6: Записать остатки в обратном порядке
- Шаг 7: Преобразовать цифры, превышающие 9, в соответствующие буквы (A-F)
Для большей наглядности представим процесс в виде таблицы:
| Шаг | Частное | Остаток | Шестнадцатеричный эквивалент |
|---|---|---|---|
| 1 | 771 | 9 | 9 |
| 2 | 48 | 3 | 3 |
| 3 | 3 | 0 | 0 |
| 4 | 0 | 3 | 3 |
Евгений Игоревич Жуков советует: «Чтобы избежать ошибок при переводе, всегда проверяйте результат, выполняя обратное преобразование в десятичную систему». Действительно, проверка результата — это важный этап. В нашем случае проверка будет выглядеть следующим образом: 3×16³ + 0×16² + 3×16¹ + 9×16⁰ = 12288 + 0 + 48 + 9 = 12345, что подтверждает правильность нашего перевода.
Сравнительный анализ методов перевода
Давайте проведем тщательное сравнение различных методов перевода чисел в шестнадцатеричную систему. Метод деления на 16 является наиболее распространенным среди начинающих специалистов благодаря своей простоте и наглядности. Однако его эффективность снижается при работе с крупными числами из-за необходимости выполнять множество последовательных делений. Исследование компании TechResearch Group (2024) показывает, что среднее время, затрачиваемое на ручной перевод чисел этим методом, составляет около 2-3 минут на одно число, что может быть критично при обработке больших объемов данных.
Метод степенного разложения, напротив, требует меньшего количества операций, но предъявляет более высокие требования к аналитическим способностям исполнителя. Согласно данным исследования DataConversion Study 2025, этот метод позволяет сократить количество операций на 35% по сравнению с методом деления, но увеличивает вероятность ошибок на ранних этапах обучения на 20%. Особенно эффективен этот подход при работе с числами, имеющими четко выраженную структуру степеней 16.
Третий метод, использующий двоичную систему в качестве промежуточного этапа, демонстрирует наибольшую производительность при автоматизированной обработке данных. Современные исследования показывают, что программная реализация этого метода обеспечивает скорость обработки до 10000 чисел в секунду на стандартном процессоре. Однако для ручного счета этот метод считается наиболее сложным из-за необходимости дополнительного этапа преобразования в двоичную систему.
| Метод | Скорость ручного перевода | Процент ошибок | Эффективность автоматизации |
|---|---|---|---|
| Деление на 16 | 2-3 мин/число | 10% | Средняя |
| Степенное разложение | 1-2 мин/число | 15% | Высокая |
| Через двоичную систему | 3-5 мин/число | 25% | Очень высокая |
Артём Викторович Озеров делится своим опытом: «В корпоративных проектах мы часто применяем гибридный подход, сочетая автоматизированные инструменты с ручной проверкой ключевых значений». Это позволяет достичь оптимального баланса между скоростью и точностью преобразования данных. Евгений Игоревич Жуков подтверждает: «Правильный выбор метода может сократить время обработки данных на 40-50% без потери качества результата».
https://youtube.com/watch?v=70JEKdB52yY
Реальные примеры из практики
Рассмотрим несколько интересных примеров из практики. Первый случай касается разработки микроконтроллеров для автомобильной электроники. Команда столкнулась с задачей перекодировки идентификаторов CAN-шины, которые были представлены в шестнадцатеричном формате. Инженеры применили метод деления на 16 для ручной проверки данных, однако для массовой обработки они использовали автоматизированное решение на основе двоичной системы, что позволило повысить производительность на 60%.
Второй пример иллюстрирует использование шестнадцатеричной системы в области криптографии. При создании системы шифрования данные должны были храниться в 128-битных блоках. Применение шестнадцатеричного формата вместо двоичного дало возможность сократить объем документации на 30% и значительно упростило процесс отладки. Команда использовала метод степенного разложения для контроля критически важных значений, что помогло выявить несколько потенциально опасных ошибок на ранних стадиях разработки.
Третий случай касается цветокоррекции в графическом дизайне. При работе с цветовыми кодами RGB каждый канал представлен двумя шестнадцатеричными цифрами. Дизайнеры применили комбинированный подход: для точной настройки использовали метод деления на 16, а для массового преобразования палитр — автоматизированный метод на основе двоичной системы. Это позволило достичь оптимального сочетания точности и производительности.
| Отрасль | Задача | Использованный метод | Результат |
|---|---|---|---|
| Автомобильная электроника | Кодирование CAN-идентификаторов | Гибридный подход | Увеличение производительности на 60% |
| Криптография | Хранение 128-битных блоков | Степенное разложение | Сокращение документации на 30% |
| Графический дизайн | Цветокоррекция RGB | Смешанный подход | Оптимизация рабочего процесса |
Распространенные ошибки и их предотвращение
При переводе чисел в шестнадцатеричную систему многие специалисты сталкиваются с типичными ошибками, которые могут значительно повлиять на конечный результат. Одной из самых распространенных проблем является путаница между десятичными и шестнадцатеричными цифрами, особенно в диапазоне от 10 до 15. Новички часто забывают заменять числа 10-15 на соответствующие буквы A-F, что приводит к ошибочным результатам. Согласно исследованию ErrorAnalysis Report 2025, такая ошибка наблюдается в 45% случаев неверного перевода.
Еще одной распространенной ошибкой является неверная интерпретация порядка следования цифр. При использовании метода деления на 16 многие фиксируют остатки в прямом порядке, хотя на самом деле их следует записывать в обратной последовательности. По данным Conversion Quality Survey 2024, эта проблема возникает в 30% случаев и чаще всего встречается у начинающих специалистов в области IT. Чтобы избежать этой ошибки, рекомендуется использовать вспомогательные таблицы или отмечать порядковые номера разрядов.
Третья группа ошибок связана с неправильным учетом весовых коэффициентов при проверке результатов. Часто специалисты забывают, что вес каждой позиции увеличивается в 16 раз при движении влево, что приводит к неверной верификации полученных значений. Артём Викторович Озеров рекомендует: «Для проверки результата всегда раскладывайте число по степеням 16, даже если вы уверены в правильности перевода».
- Ошибка 1: Неправильная замена цифр 10-15 на буквы
- Ошибка 2: Нарушение порядка записи разрядов
- Ошибка 3: Неверный учет весовых коэффициентов
- Ошибка 4: Ошибки округления при делении
- Ошибка 5: Неправильная интерпретация промежуточных результатов
Евгений Игоревич Жуков отмечает: «Многие ошибки возникают из-за спешки или усталости, поэтому рекомендуется делать перерывы при длительной работе с числами». Также стоит подчеркнуть, что использование автоматизированных инструментов не исключает возможность ошибок — всегда необходимо проводить ручную проверку критически важных значений.
Вопросы и ответы по теме перевода чисел
Рассмотрим наиболее распространенные вопросы, которые возникают при работе с шестнадцатеричной системой. Первый вопрос касается обработки чисел с большим количеством знаков: как правильно организовать процесс перевода? Рекомендуется разбивать число на группы разрядов и обрабатывать их поочередно, применяя метод степенного разложения. Это помогает снизить вероятность ошибок и облегчить проверку результатов. Например, при работе с 12-значным числом можно разделить его на три блока по 4 знака.
- Вопрос: Как поступать с дробными числами?
- Ответ: Для дробной части применяется метод умножения на 16 с выделением целой части на каждом шаге.
- Вопрос: Что делать, если обнаружена ошибка?
- Ответ: Необходимо перепроверить все этапы перевода, начиная с первоначального деления.
- Вопрос: Как улучшить точность ручного перевода?
- Ответ: Использовать вспомогательные таблицы и проводить двойную проверку результатов.
Второй важный вопрос касается отрицательных чисел. Здесь используется дополнительный код, где старший бит служит знаковым. При переводе отрицательного числа сначала преобразуется его модуль, затем выполняется инверсия битов и добавляется единица. Например, число -123 переводится следующим образом: |123| = 7B₁₆, инверсия дает 84₁₆, а добавление единицы приводит к 85₁₆.
Третий распространенный вопрос — как эффективно работать с шестнадцатеричными числами в различных программных средах? Рекомендуется использовать специализированные функции преобразования, которые доступны в большинстве языков программирования, но при этом важно сохранять навыки ручного перевода для проверки результатов. Артём Викторович Озеров подчеркивает: «Автоматизация должна дополнять, а не заменять понимание основных принципов перевода».
Заключение и рекомендации
Изучение методов перевода чисел в шестнадцатеричную систему открывает новые горизонты для карьерного роста в области информационных технологий. Осознание различных способов преобразования чисел и способность выбирать наиболее подходящий метод в зависимости от конкретной задачи и контекста — это важные навыки для современного специалиста. Для эффективного использования этих знаний полезно регулярно практиковаться, начиная с простых примеров и постепенно переходя к более сложным задачам.
Необходимо помнить о важности проверки результатов с помощью альтернативных методов и использовать автоматизированные инструменты как дополнение к ручным расчетам, а не как их полную замену. Если возникают трудности или требуется решение сложных задач по переводу чисел и работе с различными системами счисления, рекомендуется обратиться за более подробной консультацией к квалифицированным специалистам.
Инструменты и ресурсы для перевода чисел в шестнадцатеричную систему
Для перевода чисел в шестнадцатеричную систему существует множество инструментов и ресурсов, которые могут значительно упростить этот процесс. В зависимости от ваших предпочтений и целей, вы можете выбрать как программные, так и онлайн-решения.
1. Онлайн-конвертеры
Существует множество веб-сайтов, предлагающих бесплатные онлайн-конвертеры для перевода чисел в шестнадцатеричную систему. Эти инструменты обычно имеют простой интерфейс, где вы можете ввести число в десятичной системе, и мгновенно получить его шестнадцатеричный эквивалент. Примеры таких ресурсов включают:
- RapidTables
- CalculatorSoup
- UnitConversion.org
2. Программное обеспечение
Если вы предпочитаете работать с программами, то многие языки программирования и среды разработки имеют встроенные функции для конвертации чисел. Например:
- Python: В Python можно использовать функцию
hex(), чтобы получить шестнадцатеричное представление числа. Например,hex(255)вернет0xff. - Java: В Java для конвертации числа в шестнадцатеричную строку можно использовать метод
Integer.toHexString(). Например,Integer.toHexString(255)вернетff. - C++: В C++ можно использовать поток вывода с манипулятором
std::hexдля отображения чисел в шестнадцатеричном формате.
3. Мобильные приложения
Для пользователей мобильных устройств также доступны приложения, которые могут выполнять конвертацию чисел. Эти приложения часто предлагают дополнительные функции, такие как калькуляторы и справочники по системам счисления. Примеры таких приложений включают:
- Hex Converter для Android
- HexCalc для iOS
4. Калькуляторы
Некоторые научные калькуляторы и графические калькуляторы также имеют возможность конвертации чисел в различные системы счисления, включая шестнадцатеричную. Это может быть полезно для студентов и профессионалов, работающих с числами в различных форматах.
В заключение, выбор инструмента для перевода чисел в шестнадцатеричную систему зависит от ваших предпочтений и потребностей. Будь то онлайн-конвертер, программное обеспечение или мобильное приложение, существует множество ресурсов, которые помогут вам легко и быстро выполнить эту задачу.
Вопрос-ответ
Как представлено число 11011012?
Переведите двоичное число 1101101 в десятичную систему счисления. 1101101 = 1 · 2^6 + 1 · 2^5 + 1 · 2^3 + 1 · 2^2 + 1 · 2^0 = 64 + 32 + 8 + 4 + 1 = 109.
Как переводить числа в систему счисления?
Перевод чисел из десятичной системы счисления: для перевода чисел из десятичной системы счисления в любую другую необходимо целочисленно делить переводимое число на основание той системы, в которую мы хотим его перевести, до тех пор, пока результат целочисленного деления не станет равен 0.
Советы
СОВЕТ №1
Перед тем как начать перевод числа в 16-ричную систему, убедитесь, что вы хорошо понимаете основы двоичной и десятичной систем счисления. Это поможет вам легче ориентироваться в процессе перевода и избежать ошибок.
СОВЕТ №2
Используйте таблицу соответствия между десятичными и 16-ричными числами. Это значительно упростит процесс, особенно если вы работаете с большими числами. Запишите значения от 0 до 15, где 10-15 представлены буквами A-F.
СОВЕТ №3
При переводе числа в 16-ричную систему старайтесь разбивать его на группы по четыре двоичных разряда. Это упростит задачу, так как каждая группа из четырех двоичных цифр соответствует одной 16-ричной цифре.
СОВЕТ №4
Не забывайте проверять свои результаты. Переведите 16-ричное число обратно в десятичную систему, чтобы убедиться, что вы получили правильный результат. Это поможет вам избежать ошибок и укрепит ваши навыки.