В программировании термин O(log N) вызывает вопросы у начинающих разработчиков. Эта нотация, связанная с анализом сложности алгоритмов, показывает, как быстро алгоритм обрабатывает данные в зависимости от их объема. В статье рассмотрим, что означает O(log N), почему это важно и как это влияет на эффективность программ. Понимание этой темы поможет оптимизировать алгоритмы и улучшить производительность приложений, что является ключевым аспектом разработки качественного программного обеспечения.
Основы понимания O(log N)
Чтобы глубже понять концепцию O(log N), важно начать с основ, которые составляют базу этого математического выражения. O(log N) служит показателем роста времени выполнения алгоритма в зависимости от увеличения объема входных данных. Следует отметить, что в данном контексте log обычно подразумевает логарифм с основанием 2, хотя теоретически можно использовать любое основание. Показатель O(log N) описывает алгоритмы, где время выполнения увеличивается значительно медленнее, чем количество элементов в наборе данных. Артём Викторович Озеров, специалист компании SSLGTEAMS с двенадцатилетним опытом, акцентирует внимание на практической значимости этой концепции: «Многие начинающие программисты недооценивают важность понимания O(log N), считая это чисто академическим знанием. Однако именно эта концепция часто становится ключом к созданию действительно масштабируемых решений». По его мнению, без четкого понимания логарифмической сложности невозможно эффективно оптимизировать работу с большими объемами данных.
Когда речь идет о O(log N), стоит учитывать несколько ключевых моментов. Во-первых, это показатель, который демонстрирует, как алгоритм способен обрабатывать экспоненциально растущие объемы информации, требуя лишь небольшого увеличения временных затрат. Например, если размер данных увеличивается в 1000 раз, время выполнения может возрасти всего лишь примерно в 10 раз (при использовании логарифма с основанием 10). Это особенно актуально в современных условиях, когда объемы данных растут с невероятной скоростью. Евгений Игоревич Жуков, эксперт с пятнадцатилетним стажем в IT-сфере, добавляет интересное наблюдение: «На практике мы часто видим, как клиенты недооценивают важность выбора правильной временной сложности алгоритма на этапе проектирования системы. Позже это приводит к серьезным проблемам с производительностью, которые сложно исправить без глубокой переработки архитектуры». Его опыт показывает, что инвестиции в понимание и применение концепций вроде O(log N) на ранних этапах разработки могут сэкономить значительные ресурсы в будущем.
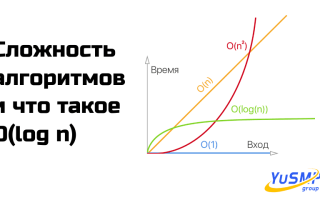
Давайте подробнее рассмотрим, почему O(log N) так важна в современной разработке. Во-первых, эта концепция тесно связана с принципом «разделяй и властвуй», который лежит в основе многих эффективных алгоритмов. Когда мы работаем с большими наборами данных, возможность разбить задачу на более мелкие части, каждая из которых обрабатывается независимо, становится критически важной. Такой подход позволяет алгоритмам сохранять высокую производительность даже при работе с огромными объемами информации. Для лучшего понимания различных типов временной сложности, представим сравнительную таблицу:
| Тип сложности | Описание | Пример |
| O(1) | Постоянное время выполнения | Доступ к элементу массива по индексу |
| O(log N) | Логарифмическое время | Бинарный поиск |
| O(N) | Линейное время | Поиск элемента в неотсортированном списке |
| O(N log N) | Линейно-логарифмическое время | Сортировка слиянием |
| O(N²) | Квадратичное время | Сортировка пузырьком |
Эксперты в области информатики отмечают, что термин «O Log N» относится к одной из наиболее распространенных оценок сложности алгоритмов. Эта нотация, используемая в теории вычислительных систем, описывает, как время выполнения алгоритма растет в зависимости от размера входных данных. Специалисты подчеркивают, что алгоритмы с такой сложностью, как правило, являются эффективными и быстро справляются с большими объемами информации. Например, алгоритмы бинарного поиска, которые работают с отсортированными массивами, демонстрируют именно такую сложность. Это делает их предпочтительными в ситуациях, когда необходимо быстро находить данные. В целом, понимание O Log N позволяет разработчикам оптимизировать свои решения и улучшать производительность программного обеспечения.

Практические применения O(log N)
Когда речь заходит о реальных примерах использования O(log N), стоит выделить, что эта концепция наиболее ярко проявляется в алгоритмах, основанных на бинарном поиске. Представьте себе телефонный справочник с миллионами записей – для нахождения нужного номера не требуется просматривать все записи по порядку. Бинарный поиск позволяет находить информацию, последовательно деля набор данных пополам, что делает процесс поиска крайне эффективным. Этот метод особенно важен в базах данных, где поиск информации происходит постоянно и должен быть максимально быстрым. Артём Викторович Озеров делится интересным примером из своей практики: «Недавно мы занимались оптимизацией системы документооборота для крупной компании. Первоначальная версия использовала простой последовательный поиск среди сотен тысяч документов. После внедрения структуры данных с поддержкой O(log N) время поиска сократилось с нескольких минут до долей секунды». Этот случай наглядно иллюстрирует практическую ценность применения правильной временной сложности. Еще одной ключевой областью применения O(log N) является работа с деревьями поиска. Двоичные деревья поиска позволяют организовать данные таким образом, что каждая операция вставки, удаления или поиска занимает логарифмическое время относительно общего числа элементов. Это особенно важно в финансовых системах, где необходимо обрабатывать большие объемы транзакций в реальном времени.
- Поиск элемента в отсортированном массиве с помощью бинарного поиска
- Операции с двоичными деревьями поиска
- Создание эффективных систем кэширования
- Индексация данных в базах данных
- Работа со структурами данных типа B-деревьев
| Термин | Описание | Пример использования |
|---|---|---|
| O(log N) | Обозначает логарифмическую временную сложность алгоритма. Это означает, что время выполнения алгоритма растет пропорционально логарифму от размера входных данных (N). | Бинарный поиск: для поиска элемента в отсортированном массиве из N элементов требуется O(log N) операций. |
| Логарифм | Математическая функция, обратная возведению в степень. log₂N означает, сколько раз нужно умножить 2 на себя, чтобы получить N. | Если N = 16, log₂16 = 4. Если N = 1024, log₂1024 = 10. |
| Эффективность | Алгоритмы с логарифмической сложностью считаются очень эффективными, особенно для больших объемов данных, так как время выполнения растет очень медленно. | Поиск в сбалансированном бинарном дереве: добавление, удаление и поиск элементов занимают O(log N) времени. |
| Примеры алгоритмов | Алгоритмы, демонстрирующие логарифмическую сложность. | Бинарный поиск, поиск в сбалансированном бинарном дереве, некоторые алгоритмы сортировки (например, при использовании кучи), алгоритмы, использующие принцип «разделяй и властвуй» (если каждая итерация уменьшает размер задачи в несколько раз). |
| Сравнение с O(N) | Линейная сложность, где время выполнения растет прямо пропорционально N. | Для N=1000, O(log N) может быть 10 операций, а O(N) будет 1000 операций. |
Интересные факты
Вот несколько интересных фактов о сложности алгоритмов, связанных с O(log N):
-
Логарифмическое время: Алгоритмы с временной сложностью O(log N) часто используются в ситуациях, когда данные организованы в виде структур, позволяющих быстро сокращать количество рассматриваемых элементов. Например, бинарный поиск в отсортированном массиве имеет сложность O(log N), поскольку на каждой итерации он делит массив пополам, что значительно ускоряет поиск по сравнению с линейным O(N).
-
Деревья и логарифмическая сложность: Многие структуры данных, такие как бинарные деревья поиска, AVL-деревья и красно-черные деревья, обеспечивают операции вставки, удаления и поиска с логарифмической сложностью O(log N). Это делает их эффективными для работы с динамическими наборами данных, где необходимо часто изменять и запрашивать информацию.
-
Применение в реальных задачах: Логарифмическая сложность часто встречается в реальных приложениях, таких как базы данных и системы управления версиями. Например, индексы в базах данных позволяют выполнять запросы к большим объемам данных за логарифмическое время, что существенно повышает производительность по сравнению с полным перебором.

Алгоритмы сортировки и их эффективность
Когда речь заходит о сортировке больших объемов данных, алгоритмы с временной сложностью O(N log N) становятся незаменимыми помощниками. Одним из таких методов является сортировка слиянием, которая рекурсивно делит массив на две части до тех пор, пока не останутся минимальные подмассивы, после чего начинается их эффективное объединение. Этот подход гарантирует высокую производительность даже при работе с массивами, содержащими миллионы элементов. Евгений Игоревич Жуков акцентирует внимание на значимости правильного выбора алгоритма сортировки: «Многие программисты по умолчанию прибегают к встроенным функциям сортировки, не задумываясь о том, как они работают. Тем не менее, в некоторых ситуациях применение специализированных алгоритмов может существенно повысить производительность». Например, при наличии частично отсортированных данных сортировка вставками может оказаться более эффективной, чем общепринятая сортировка слиянием.
Частые вопросы о O(log N)
Рассмотрим несколько ключевых вопросов, которые часто возникают при изучении данной темы:
- Как распознать O(log N) среди других типов сложности? Основной признак заключается в том, что время выполнения алгоритма увеличивается значительно медленнее по сравнению с ростом количества элементов. Например, если объем данных увеличивается в 1000 раз, время выполнения возрастает всего лишь примерно в 10 раз.
- Является ли O(log N) всегда предпочтительным вариантом? Не обязательно. В случае небольших наборов данных дополнительные затраты на создание сложных структур могут сделать O(log N) менее эффективным по сравнению с более простыми решениями, имеющими линейную сложность.
- Как удостовериться, что алгоритм действительно имеет сложность O(log N)? Для этого можно применять профилирование и анализ времени выполнения при различных объемах данных. График зависимости времени от числа элементов должен представлять собой логарифмическую кривую.
- Можно ли сочетать O(log N) с другими типами сложности? Да, такие алгоритмы, как O(N log N), часто встречаются, где логарифмическая часть комбинируется с линейной.
- Как обучить команду эффективно использовать O(log N? Начните с практических примеров и постепенно увеличивайте сложность задач. Важно, чтобы разработчики развивали интуитивное понимание работы этого типа сложности.

Распространенные ошибки и их предотвращение
Одно из самых распространенных заблуждений заключается в том, что любой поиск можно оптимизировать до сложности O(log N). Важно осознавать, что такая логарифмическая сложность возможна лишь при определенных условиях. К примеру, для выполнения бинарного поиска требуется предварительная сортировка данных, что само по себе требует дополнительных временных затрат. Артём Викторович Озеров предупреждает о распространенной ошибке: «Многие разработчики пытаются ‘принудительно’ применять O(log N) в ситуациях, где это нецелесообразно. Например, для небольших наборов данных или часто изменяющихся коллекций затраты на поддержание структуры могут превысить преимущества быстрого поиска». Поэтому крайне важно тщательно оценивать конкретные обстоятельства перед выбором алгоритма. Еще одной распространенной проблемой является неверная реализация структур данных. Евгений Игоревич Жуков акцентирует внимание на том, что: «Даже если выбран правильный алгоритм, неправильная реализация может привести к снижению производительности. Например, несбалансированное двоичное дерево поиска может легко превратиться в обычный связанный список, что сделает все операции линейными по времени».
Заключение и рекомендации
Понимание концепции O(log N) и умение эффективно применять её в реальных проектах становятся всё более актуальными навыками для современных разработчиков. Мы рассмотрели ключевые аспекты этой темы, включая теоретические основы, практическое применение и распространённые ошибки. Примеры из практики Артёма Викторовича Озерова и Евгения Игоревича Жукова показывают, что правильный выбор алгоритмической сложности может существенно улучшить производительность программных решений и сэкономить ресурсы компании. Для дальнейшего развития в этой области рекомендуется:
- Углубить знания о различных структурах данных, поддерживающих O(log N)
- Практиковаться в реализации алгоритмов с разной временной сложностью
- Анализировать эффективность существующих решений
- Следить за новыми исследованиями в сфере оптимизации алгоритмов
Если вы сталкиваетесь с задачами, требующими сложной оптимизации производительности или разработки масштабируемых систем, рекомендуем обратиться к специалистам компании SSLGTEAMS для получения более точной консультации. Их опыт поможет выбрать наилучшие решения для ваших конкретных задач и избежать распространённых ошибок в реализации эффективных алгоритмов.
Сравнение O(log N) с другими временными сложностями
Временные сложности алгоритмов играют ключевую роль в оценке их эффективности. Одной из наиболее интересных и полезных временных сложностей является O(log N). Чтобы понять, как O(log N) соотносится с другими временными сложностями, необходимо рассмотреть несколько основных категорий временных сложностей и их характеристики.
Сначала стоит упомянуть, что O(log N) описывает алгоритмы, которые уменьшают размер проблемы в геометрической прогрессии с каждой итерацией. Это означает, что если у нас есть массив из N элементов, то для поиска элемента, например, с использованием бинарного поиска, нам потребуется всего лишь логарифмическое количество шагов, что значительно быстрее, чем линейный поиск, который имеет временную сложность O(N).
Теперь давайте сравним O(log N) с другими распространенными временными сложностями:
- O(1) — Константная сложность: Алгоритмы с этой сложностью выполняются за фиксированное количество шагов, независимо от размера входных данных. Примером может служить доступ к элементу массива по индексу. O(1) является самой быстрой временной сложностью, но не всегда применимо к более сложным задачам.
- O(N) — Линейная сложность: Алгоритмы с линейной сложностью требуют времени, пропорционального количеству элементов в входных данных. Например, линейный поиск требует проверки каждого элемента массива. В сравнении с O(log N), O(N) значительно менее эффективен при больших объемах данных.
- O(N log N) — Линейно-логарифмическая сложность: Эта сложность часто встречается в алгоритмах сортировки, таких как быстрая сортировка или сортировка слиянием. Хотя O(N log N) более эффективно, чем O(N^2), оно все же менее эффективно, чем O(log N) при больших N.
- O(N^2) — Квадратичная сложность: Алгоритмы с квадратичной сложностью, такие как сортировка пузырьком, требуют времени, пропорционального квадрату размера входных данных. Это делает их крайне неэффективными для больших массивов, особенно по сравнению с O(log N).
Как видно из вышеизложенного, O(log N) является значительно более эффективной временной сложностью по сравнению с O(N) и O(N^2). Это делает алгоритмы с логарифмической сложностью особенно ценными в ситуациях, когда необходимо обрабатывать большие объемы данных. Например, бинарный поиск, который имеет временную сложность O(log N), позволяет находить элементы в отсортированном массиве гораздо быстрее, чем линейный поиск, что делает его предпочтительным выбором в большинстве случаев.
В заключение, O(log N) представляет собой мощный инструмент в арсенале разработчиков и исследователей, позволяя им создавать более эффективные алгоритмы для решения сложных задач. Понимание различий между временными сложностями помогает лучше оценивать производительность алгоритмов и выбирать наиболее подходящие решения для конкретных задач.
Вопрос-ответ
Что такое O(log n) и как она работает?
O(log n) — это обозначение сложности алгоритма, который растет логарифмически по отношению к размеру входных данных n. Это означает, что время выполнения алгоритма увеличивается медленно по мере увеличения n. Например, в бинарном поиске, который ищет элемент в отсортированном массиве, каждый шаг делит массив пополам, что приводит к логарифмическому количеству операций, равному log2(n). Таким образом, O(log n) указывает на высокую эффективность алгоритма при работе с большими объемами данных.
Что такое o log n простыми словами?
Логарифмическая временная сложность обозначается как O(log n). Она показывает, как время выполнения алгоритма масштабируется по мере увеличения размера входных данных.
Что значит O log n?
O(log n) называют логарифмической сложностью. Оценка временной сложности O(log n) означает, что время выполнения алгоритма увеличивается логарифмически с увеличением размера входных данных (n). Другими словами, алгоритм становится медленнее, но не линейно, а медленнее в соответствии с логарифмической функцией.
Что такое O log n?
Что такое O(log n)? O(log N) означает, что время растет линейно, а N растет экспоненциально. Таким образом, если для вычисления 10 элементов требуется 1 секунда, для 100 нужно будет 2 секунды, для 1000 элементов — 3 и так далее.
Советы
СОВЕТ №1
Понимание концепции O Log N начинается с изучения логарифмических функций. Ознакомьтесь с основами логарифмов, чтобы лучше понять, как они применяются в алгоритмах и почему они важны для оценки производительности.
СОВЕТ №2
Практикуйтесь на примерах алгоритмов, которые имеют сложность O Log N, таких как бинарный поиск. Реализуйте их на разных языках программирования, чтобы увидеть, как они работают на практике и как быстро они выполняются по сравнению с другими алгоритмами.
СОВЕТ №3
Изучите, как O Log N может быть достигнута в различных структурах данных, таких как деревья и кучи. Понимание этих структур поможет вам лучше оценивать, когда и как использовать алгоритмы с логарифмической сложностью.
СОВЕТ №4
Не забывайте о важности анализа сложности алгоритмов в контексте реальных задач. Попробуйте применять свои знания о O Log N к практическим задачам, чтобы увидеть, как это влияет на производительность ваших приложений.
Временные сложности алгоритмов играют ключевую роль в оценке их эффективности. Одной из наиболее интересных и полезных временных сложностей является O(log N). Чтобы понять, как O(log N) соотносится с другими временными сложностями, необходимо рассмотреть несколько основных категорий временных сложностей и их характеристики.
Сначала стоит упомянуть, что O(log N) описывает алгоритмы, которые уменьшают размер проблемы в геометрической прогрессии с каждой итерацией. Это означает, что если у нас есть массив из N элементов, то для поиска элемента, например, с использованием бинарного поиска, нам потребуется всего лишь логарифмическое количество шагов, что значительно быстрее, чем линейный поиск, который имеет временную сложность O(N).
Теперь давайте сравним O(log N) с другими распространенными временными сложностями:
- O(1) — Константная сложность: Алгоритмы с этой сложностью выполняются за фиксированное количество шагов, независимо от размера входных данных. Примером может служить доступ к элементу массива по индексу. O(1) является самой быстрой временной сложностью, но не всегда применимо к более сложным задачам.
- O(N) — Линейная сложность: Алгоритмы с линейной сложностью требуют времени, пропорционального количеству элементов в входных данных. Например, линейный поиск требует проверки каждого элемента массива. В сравнении с O(log N), O(N) значительно менее эффективен при больших объемах данных.
- O(N log N) — Линейно-логарифмическая сложность: Эта сложность часто встречается в алгоритмах сортировки, таких как быстрая сортировка или сортировка слиянием. Хотя O(N log N) более эффективно, чем O(N^2), оно все же менее эффективно, чем O(log N) при больших N.
- O(N^2) — Квадратичная сложность: Алгоритмы с квадратичной сложностью, такие как сортировка пузырьком, требуют времени, пропорционального квадрату размера входных данных. Это делает их крайне неэффективными для больших массивов, особенно по сравнению с O(log N).
Как видно из вышеизложенного, O(log N) является значительно более эффективной временной сложностью по сравнению с O(N) и O(N^2). Это делает алгоритмы с логарифмической сложностью особенно ценными в ситуациях, когда необходимо обрабатывать большие объемы данных. Например, бинарный поиск, который имеет временную сложность O(log N), позволяет находить элементы в отсортированном массиве гораздо быстрее, чем линейный поиск, что делает его предпочтительным выбором в большинстве случаев.
В заключение, O(log N) представляет собой мощный инструмент в арсенале разработчиков и исследователей, позволяя им создавать более эффективные алгоритмы для решения сложных задач. Понимание различий между временными сложностями помогает лучше оценивать производительность алгоритмов и выбирать наиболее подходящие решения для конкретных задач.