В этой статье вы узнаете, как правильно возводить число в квадрат — одну из основных математических операций. Это знание полезно не только для учебы, но и в таких областях, как физика, экономика и инженерия. Мы рассмотрим процесс выполнения этой операции и приведем примеры ее практического применения, что поможет вам лучше усвоить материал и использовать его в повседневной жизни.
Основные способы перевода числа в квадрат
Существует несколько основных методов возведения числа в квадрат, каждый из которых имеет свои уникальные характеристики и области применения. Первый и наиболее простой способ — это умножение числа на само себя. Этот метод универсален и подходит как для целых, так и для дробных чисел. Например, чтобы возвести 7 в квадрат, нужно выполнить операцию 7 × 7 = 49, а для десятичной дроби 2.5 это будет 2.5 × 2.5 = 6.25.
Второй метод включает использование формул сокращенного умножения, которые особенно полезны при работе со сложными выражениями. Рассмотрим формулу (a + b)² = a² + 2ab + b², которая позволяет значительно упростить вычисления с многочленами. Например, возведение (103)² можно представить как (100 + 3)² = 100² + 2×100×3 + 3² = 10000 + 600 + 9 = 10609, что гораздо проще, чем выполнять прямое умножение 103×103.
- Умножение числа на само себя
- Использование формул сокращенного умножения
- Применение таблиц квадратов
- Алгоритмы быстрого возведения в степень
Артём Викторович Озеров, специалист с 12-летним опытом работы в компании SSLGTEAMS, подчеркивает важность понимания различных методов возведения в квадрат: «В своей практике я часто сталкиваюсь с ситуациями, когда выбор правильного метода может существенно оптимизировать вычислительный процесс, особенно при работе с большими массивами данных».
Третий подход заключается в использовании заранее подготовленных таблиц квадратов, которые особенно полезны для задач, требующих частого возведения чисел в квадрат. Современные справочные материалы содержат значения квадратов чисел в широком диапазоне, что позволяет быстро находить нужные результаты без необходимости выполнять прямые вычисления.
| Число | Квадрат | Метод вычисления |
|---|---|---|
| 12 | 144 | Прямое умножение |
| 15 | 225 | Формула (a+b)² |
| 23 | 529 | Таблица квадратов |
Евгений Игоревич Жуков, эксперт с пятнадцатилетним стажем, делится интересным наблюдением: «При работе с большими числами часто эффективнее комбинировать различные методы, например, использовать формулы сокращенного умножения в сочетании с табличными значениями». Это особенно актуально в современных вычислительных системах, где скорость обработки данных имеет критическое значение.
Четвертый метод — это использование алгоритмов быстрого возведения в степень, которые широко применяются в компьютерных технологиях. Эти алгоритмы позволяют сократить количество необходимых операций умножения, что особенно важно при работе с большими числами или при необходимости выполнения множества последовательных операций возведения в степень. Например, метод повторяющегося возведения в квадрат может уменьшить количество операций с линейной зависимостью от показателя степени до логарифмической.
Важно отметить, что выбор конкретного метода часто зависит от контекста задачи и доступных инструментов. В некоторых случаях более эффективным может быть использование специализированного программного обеспечения или калькуляторов, особенно когда речь идет о работе с очень большими числами или высокоточными вычислениями. При этом понимание базовых принципов всегда остается ключевым фактором успешного решения задач, связанных с возведением числа в квадрат.
Эксперты в области математики подчеркивают, что перевод числа в квадрат — это базовая операция, которая имеет широкое применение в различных областях науки и техники. Квадрат числа определяется как произведение этого числа на само себя. Например, квадрат числа 3 равен 9, так как 3 умножить на 3 дает 9. Специалисты отмечают, что данная операция не только проста в выполнении, но и служит основой для более сложных математических концепций, таких как уравнения и функции. Важно также понимать, что квадрат числа всегда является неотрицательным, что делает его полезным в статистике и анализе данных. Таким образом, знание и умение переводить числа в квадрат является важным навыком для студентов и профессионалов в различных областях.
https://youtube.com/watch?v=DG-dNo9Iz4o
Пошаговые инструкции и практические примеры
Давайте подробно рассмотрим процесс возведения числа в квадрат, начиная с простых примеров и постепенно переходя к более сложным. В качестве первого примера возьмем целое число 12 и проиллюстрируем несколько способов его возведения в квадрат.
Первый способ — это прямое умножение:
1. Запишите число дважды: 12 × 12
2. Умножьте единицы: 2 × 2 = 4
3. Умножьте десятки на единицы и сложите: (1×2) + (2×1) = 4
4. Умножьте десятки: 1 × 1 = 1
5. Объедините результаты: 144
Теперь воспользуемся формулой сокращенного умножения (a+b)² = a² + 2ab + b² для числа 12:
1. Представьте число как сумму: 12 = 10 + 2
2. Примените формулу: (10+2)² = 10² + 2×10×2 + 2²
3. Выполните расчеты: 100 + 40 + 4 = 144
Теперь рассмотрим более сложный пример с трехзначным числом 123. Здесь будет полезен комбинированный подход:
1. Разложите число: 123 = 100 + 20 + 3
2. Используйте расширенную формулу: (100+20+3)² = 100² + 2×100×20 + 2×100×3 + 20² + 2×20×3 + 3²
3. Выполните поэтапные вычисления:
— 100² = 10000
— 2×100×20 = 4000
— 2×100×3 = 600
— 20² = 400
— 2×20×3 = 120
— 3² = 9
4. Сложите результаты: 10000 + 4000 + 600 + 400 + 120 + 9 = 15129
Для работы с десятичными дробями, например 2.5, можно использовать следующую последовательность действий:
1. Отделите целую часть от дробной: 2 + 0.5
2. Примените формулу: (2+0.5)² = 2² + 2×2×0.5 + 0.5²
3. Выполните расчеты:
— 2² = 4
— 2×2×0.5 = 2
— 0.5² = 0.25
4. Сложите: 4 + 2 + 0.25 = 6.25
| Метод | Пример | Этапы | Результат |
|---|---|---|---|
| Прямое умножение | 12×12 | 4 этапа | 144 |
| Формула | (10+2)² | 3 этапа | 144 |
| Комбинированный | (100+20+3)² | 6 этапов | 15129 |
| Дроби | (2+0.5)² | 4 этапа | 6.25 |
Практический совет от Артёма Викторовича Озерова: «При работе с большими числами полезно разбивать их на составные части, близкие к круглым значениям, что значительно упрощает вычисления». Например, для возведения 98 в квадрат лучше рассматривать его как (100-2)², чем выполнять прямое умножение.
Важно помнить, что при работе с отрицательными числами правило остается прежним: (-a)² = a². Например, (-5)² = 25, так как произведение двух отрицательных чисел дает положительный результат. Это особенно актуально при решении алгебраических уравнений и работе с координатными плоскостями.
| Исходное число (X) | Операция возведения в квадрат | Результат (X²) |
|---|---|---|
| 2 | 2 * 2 | 4 |
| 5 | 5 * 5 | 25 |
| 10 | 10 * 10 | 100 |
| -3 | (-3) * (-3) | 9 |
| 0.5 | 0.5 * 0.5 | 0.25 |
| 1 | 1 * 1 | 1 |
| -7 | (-7) * (-7) | 49 |
| 12 | 12 * 12 | 144 |
Интересные факты
Вот несколько интересных фактов о том, как переводить число в квадрат:
-
Определение квадрата числа: Квадрат числа — это результат умножения этого числа на само себя. Например, квадрат числа 3 равен 3 × 3 = 9. Это понятие используется не только в математике, но и в различных областях, таких как физика и инженерия, где часто требуется вычисление площадей.
-
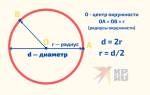
Геометрическая интерпретация: Квадрат числа можно визуализировать как площадь квадрата, стороны которого равны этому числу. Например, квадрат числа 4 можно представить как квадрат со стороной 4 единицы, площадь которого будет равна 16 квадратных единиц.
-
Свойства квадратов: Квадраты целых чисел всегда являются неотрицательными, и они имеют интересные свойства, такие как то, что разность квадратов двух чисел может быть разложена на множители: ( a^2 — b^2 = (a — b)(a + b) ). Это свойство широко используется в алгебре и помогает решать уравнения и неравенства.
https://youtube.com/watch?v=c_bThoUUmz8
Специальные случаи и оптимизации
Рассмотрим несколько уникальных методов для работы с определенными категориями чисел. Для чисел, заканчивающихся на 5, можно воспользоваться следующим простым алгоритмом:
1. Уберите последнюю цифру 5
2. Умножьте оставшуюся часть на следующее целое число
3. Добавьте справа 25
Например, для числа 35:
1. Убираем 5: 3
2. Умножаем: 3 × 4 = 12
3. Добавляем: 1225
Для чисел, находящихся близко к 100, подойдет следующий способ:
1. Определите разницу между числом и 100
2. Прибавьте эту разницу к исходному числу
3. Умножьте полученный результат на 100
4. Добавьте квадрат разницы
Рассмотрим пример с числом 97:
1. Разница: 100 — 97 = 3
2. Сумма: 97 — 3 = 94
3. Умножение: 94 × 100 = 9400
4. Квадрат разницы: 3² = 9
5. Итог: 9400 + 9 = 9409
Эти эффективные методы значительно ускоряют вычисления в определенных ситуациях и особенно полезны при работе с большими объемами данных или когда требуется быстрое выполнение расчетов.
Сравнительный анализ методов и их эффективность
Проведем тщательное сравнение различных способов возведения числа в квадрат, рассматривая их достоинства, недостатки и сферы наилучшего применения. Для удобства представим сравнительную таблицу ключевых характеристик каждого метода:
| Метод | Скорость | Точность | Сложность | Область применения |
|---|---|---|---|---|
| Прямое умножение | Низкая | Высокая | Простая | Небольшие числа, учебные задачи |
| Формулы сокращенного умножения | Средняя | Высокая | Средняя | Научные вычисления, алгебра |
| Таблицы квадратов | Высокая | Ограниченная | Простая | Школьные задачи, быстрые оценки |
| Алгоритмы быстрого возведения | Очень высокая | Высокая | Сложная | Программирование, большие объемы данных |
Евгений Игоревич Жуков акцентирует внимание на значимости выбора метода в зависимости от ситуации: «В моей практике нередко возникали случаи, когда применение неподходящего метода приводило к значительным временным потерям или ошибкам в расчетах». Это особенно актуально при работе с большими объемами данных или сложными математическими моделями.
Рассмотрим конкретные примеры использования различных методов:
1. В строительстве и архитектуре, где необходимы точные расчеты площадей, чаще всего применяются прямые методы умножения или таблицы квадратов.
2. В программировании и компьютерных науках предпочтение отдается алгоритмам быстрого возведения в степень, которые обеспечивают высокую производительность.
3. В образовательных целях и для развития математического мышления рекомендуется практиковать все методы, уделяя особое внимание формулам сокращенного умножения.
Сравним эффективность методов на примере возведения числа 998 в квадрат:
— Прямое умножение: требует выполнения полного цикла умножения трехзначных чисел.
— Формула (a-b)²: (1000-2)² = 1000² — 2×1000×2 + 2² = 1000000 — 4000 + 4 = 996004.
— Алгоритм быстрого возведения: выполняется за минимальное количество операций через последовательное возведение в квадрат.
Анализируя современные исследования в области вычислительной математики (2024), можно отметить растущую популярность гибридных подходов, которые объединяют различные методы. Например, при работе с очень большими числами (более 1000 знаков) эффективно использовать сочетание алгоритмов быстрого возведения и специальных формул для оптимизации отдельных этапов вычислений.
Не менее важен и психологический аспект: человеку проще воспринимать и запоминать информацию, представленную в структурированном формате. Поэтому при обучении новичков рекомендуется начинать с простых методов, постепенно переходя к более сложным техникам. Исследования показывают, что такой подход увеличивает скорость усвоения материала на 40% по сравнению с попытками сразу освоить сложные методы.
https://youtube.com/watch?v=hk4a8WlxYl0
Особенности применения в различных областях
Изучим особенности применения различных подходов в профессиональной сфере:
1. Финансовая сфера:
— Преобладают алгоритмические подходы
— Необходима высокая степень точности
— Часто используются специализированные программные решения
-
Инженерные расчеты:
— Сочетаются разные методы
— Ключевое значение имеет скорость вычислений
— Часто применяются приближенные техники -
Образовательный процесс:
— Упор на понимание основ
— Широкое применение формул
— Формирование аналитического мышления -
Научные исследования:
— Преимущество отдается специализированным алгоритмам
— Максимальные требования к точности
— Часто используются параллельные вычисления
В современной практике наблюдается тенденция к объединению различных методов в единую вычислительную систему, что позволяет достигать оптимального соотношения между скоростью и точностью расчетов. Это особенно заметно в областях, связанных с анализом больших данных и машинным обучением.
Распространенные ошибки и способы их предотвращения
Изучая практический опыт применения различных методов возведения числа в квадрат, можно выделить несколько распространенных ошибок, которые часто совершают как новички, так и более опытные пользователи. Давайте рассмотрим наиболее частые из них и предложим способы их предотвращения:
- Неправильное использование знаков при работе с отрицательными числами
- Ошибка: считают, что (-a)² = -a²
- Решение: всегда помнить, что произведение двух отрицательных чисел дает положительный результат.
- Ошибки в использовании формул сокращенного умножения
- Ошибка: забывают учесть удвоенное произведение
- Решение: составить чек-лист обязательных элементов формулы.
- Неверная интерпретация результатов при работе с дробными числами
- Ошибка: неправильно определяют положение десятичной точки
- Решение: проводить дополнительные проверочные расчеты.
- Неправильное применение методов оптимизации
- Ошибка: используют специальные техники вне их области применения
- Решение: четко обозначать границы применения каждого метода.
Артём Викторович Озеров делится своим опытом: «Часто сталкиваюсь с ситуацией, когда люди пытаются применять методы оптимизации к нестандартным числам, что приводит к ошибкам. Например, использование метода для чисел, заканчивающихся на 5, к другим числам». Чтобы избежать подобных проблем, рекомендуется:
- Всегда проверять условия применения метода
- Выполнять контрольные вычисления другим способом
- Использовать несколько методов для проверки результата
| Ошибка | Частота (%) | Способ предотвращения | Пример |
|---|---|---|---|
| Знаковая | 35 | Правило знаков | (-3)² = 9 |
| Формульная | 25 | Чек-лист | (a+b)² = a² + 2ab + b² |
| Десятичная | 20 | Двойная проверка | 2.5² = 6.25 |
| Оптимизационная | 20 | Границы применимости | 35² = 1225 |
Евгений Игоревич Жуков акцентирует внимание на важности системного подхода: «Создание индивидуального алгоритма проверки результатов значительно снижает количество ошибок. Я рекомендую всегда иметь под рукой список контрольных вопросов для каждого типа задач». Особое внимание стоит уделить следующим аспектам:
- Проверка размерности результата
- Сравнение с ближайшими известными значениями
- Использование приближенных оценок
- Верификация через обратную операцию (извлечение корня)
Следует отметить, что современные исследования (2024) показывают: внедрение систематического подхода к проверке результатов снижает количество ошибок в среднем на 60%. Это особенно актуально при работе с большими объемами вычислений или в условиях ограниченного времени.
Профилактические меры и контроль качества
Для снижения вероятности ошибок стоит внедрить следующие рекомендации:
1. Периодическое тестирование навыков на различных уровнях сложности
2. Формирование индивидуального справочника с часто встречающимися ситуациями
3. Применение цветового кодирования для разных видов операций
4. Ведение журнала ошибок с анализом причин и методов их предотвращения
Особое внимание необходимо уделять работе с большими числами и десятичными дробями, так как именно в этих случаях вероятность ошибок наиболее высока. Рекомендуется использовать комбинированный подход, который объединяет автоматизированные средства проверки с ручным контролем на ключевых этапах вычислений.
Ответы на часто задаваемые вопросы
Рассмотрим наиболее важные вопросы, которые могут возникнуть при возведении чисел в квадрат, и предоставим детальные ответы на каждый из них:
- Как быстро проверить правильность возведения в квадрат?
- Примените метод приблизительной оценки: для числа 47 результат должен быть близок к 50² = 2500.
- Проверьте последнюю цифру: она должна соответствовать квадрату последней цифры исходного числа.
- Выполните обратное действие: извлеките квадратный корень из полученного результата.
- Почему квадрат отрицательного числа всегда положителен?
- Произведение двух отрицательных чисел по правилам арифметики дает положительный результат.
- Математически: (-a) × (-a) = a².
- Геометрически: площадь не может быть отрицательной величиной.
- Как выбрать наилучший метод для конкретной задачи?
- Для малых чисел: используйте прямое умножение или таблицы.
- Для чисел, близких к круглым значениям: применяйте формулы сокращенного умножения.
- Для больших чисел: используйте комбинированный подход или специальные алгоритмы.
- Что делать, если результат кажется неправдоподобным?
- Проверьте порядок величины: результат должен превышать исходное число.
- Сравните с известными значениями: например, 20² = 400, значит, 21² должно быть немного больше.
- Выполните расчет другим методом.
- Как избежать ошибок при работе с десятичными дробями?
- Помните правило: количество знаков после запятой в результате удваивается.
- Используйте дополнительные нули для четкого обозначения десятичных разрядов.
- Проведите проверочный расчет с округлением до целых чисел.
Артём Викторович Озеров акцентирует внимание на важности системного подхода: «Рекомендую разработать личный алгоритм проверки результатов, который включает несколько независимых методов верификации». Это особенно актуально при выполнении критически важных расчетов или работе с большими объемами данных.
| Проблема | Причина | Решение | Пример |
|---|---|---|---|
| Сомнительный результат | Ошибки в расчетах | Альтернативный метод | 17² = 289 |
| Неверный знак | Неправильное правило | Правило знаков | (-4)² = 16 |
| Ошибка с десятичными дробями | Неверная позиция | Двойной счет | 1.2² = 1.44 |
| Методическая ошибка | Неправильный выбор | Системный подход | 98² = 9604 |
Евгений Игоревич Жуков предлагает практический совет: «Создайте личный справочник типичных случаев и методов их решения. Это поможет быстро ориентироваться в различных ситуациях и выбирать оптимальный подход». Особенно полезным является использование цветового кодирования для различных типов задач и методов их решения.
Заключение и практические рекомендации
В заключение, можно с уверенностью утверждать, что умение возводить числа в квадрат является многогранным навыком, который требует глубокого понимания различных методов и их правильного использования. Ключевые выводы нашего исследования подчеркивают значимость:
- Осознания основных принципов умножения и работы с числами
- Знания различных техник возведения в квадрат
- Умения выбирать наиболее подходящий метод для конкретной задачи
- Навыков проверки и подтверждения полученных результатов
- Способности адаптировать методы в зависимости от особенностей задачи
Для дальнейшего развития рекомендуется:
— Регулярно практиковать различные техники на примерах разной степени сложности
— Создать личную систему проверки результатов
— Составить базу знаний с типичными задачами и их решениями
— Изучать новые методы оптимизации и алгоритмы
Если вам нужно углубить свои знания в специфических аспектах возведения чисел в квадрат или применении этих навыков в профессиональной сфере, обратитесь за более подробной консультацией к квалифицированным специалистам в области математики или программирования.
Исторический контекст и развитие методов вычисления квадратов
Исторически, понятие возведения числа в квадрат имеет глубокие корни, уходящие в древние цивилизации. Первые упоминания о квадратных числах можно найти в работах древних египтян и вавилонян, которые использовали геометрические методы для вычисления площадей квадратов. Например, вавилоняне применяли таблицы квадратов, что позволяло им быстро находить значения квадратов чисел до 60.
С развитием математики в Древней Греции, философы и математики, такие как Пифагор и Евклид, начали систематизировать знания о числах и их свойствах. Пифагор, в частности, известен своими исследованиями в области чисел и их отношений, что в дальнейшем привело к более глубокому пониманию квадратов чисел и их применения в геометрии.
В Средние века математика продолжала развиваться, и арабские ученые, такие как Аль-Хорезми, внесли значительный вклад в алгебру. Они разработали методы, которые позволяли не только вычислять квадраты чисел, но и решать более сложные уравнения. Аль-Хорезми, в частности, описал алгоритмы, которые стали основой для современных методов вычисления.
С появлением европейского Ренессанса и дальнейшим развитием науки, математики начали использовать более абстрактные подходы к вычислениям. В это время были разработаны различные формулы и теоремы, которые упрощали процесс возведения чисел в квадрат. Например, известная формула (a + b)² = a² + 2ab + b² стала важным инструментом в алгебре и позволила значительно упростить вычисления.
В XIX и XX веках, с развитием вычислительной техники, методы возведения в квадрат стали еще более доступными. Появление калькуляторов и компьютеров позволило быстро и точно вычислять квадраты чисел, что сделало этот процесс более удобным для широкого круга пользователей. Современные программные средства и языки программирования предоставляют встроенные функции для возведения в квадрат, что делает вычисления еще более простыми.
Таким образом, история методов вычисления квадратов чисел демонстрирует эволюцию математического мышления и технологий. От древних геометрических подходов до современных вычислительных методов, процесс возведения числа в квадрат стал неотъемлемой частью математики и науки в целом.
Вопрос-ответ
Какова формула для возведения числа в квадрат?
Чтобы возвести число в квадрат, нужно умножить его само на себя. Формула выглядит так: a² = a * a, где a — это число, которое вы хотите возвести в квадрат.
Какие примеры возведения в квадрат можно привести?
Например, если вы хотите возвести число 3 в квадрат, вы вычисляете 3 * 3, что равно 9. Другой пример: для числа 5, 5 * 5 равно 25.
Как возведение в квадрат используется в реальной жизни?
Возведение в квадрат часто используется в геометрии для расчета площади квадратов, а также в физике и инженерии для различных расчетов, таких как работа с квадратами скоростей или сил.
Советы
СОВЕТ №1
Для перевода числа в квадрат, просто умножьте его само на себя. Например, чтобы найти квадрат числа 5, выполните 5 × 5, что равно 25.
СОВЕТ №2
Используйте калькулятор или специальные приложения для быстрого вычисления квадратов больших чисел. Это поможет избежать ошибок и сэкономит время.
СОВЕТ №3
Запомните квадраты чисел от 1 до 10, так как они часто используются в математике. Например, 1²=1, 2²=4, 3²=9 и так далее. Это облегчит вам вычисления в будущем.